题目内容
【题目】如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为 . 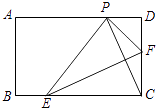
【答案】![]() ≤x≤3
≤x≤3
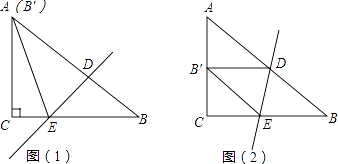
【解析】解:如图1,当点E与点B重合时,根据翻折对称性可得
BP=BC=5,
在Rt△ABP中,AP= ![]() =4,
=4,
∴PD=AD﹣AP=5﹣4=1,
在Rt△PDF中,PF2=DP2+DF2 ,
即PF2=12+(3﹣PF)2 ,
解得PF= ![]() ,
,
即CF的最小值是 ![]() ;
;
如图2,当点F与点D重合时,CF的值最大是3.
故x的取值范围为 ![]() ≤x≤3.
≤x≤3.
所以答案是: ![]() ≤x≤3.
≤x≤3.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目