题目内容
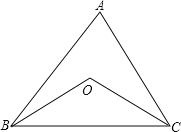
【题目】如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC。
【答案】(1) 40°;(2) 130°
【解析】
试题(1)连接AO,利用等腰三角形的对称性即可求得∠OAC的度数;(2)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
试题解析:
(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°。

练习册系列答案
相关题目
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙两个小组各项得分如下表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果研究报告、小组展示、答辩按照4:3:3计算成绩,哪个小组的成绩最高?