题目内容
若a，b，c表示△ABC的三边，且满足
+|a-3|+（b-4）2=0，则△ABC的形状是
- A.等腰三角形
- B.直角三角形
- C.等腰直角三角形
- D.等边三角形
B
分析：利用非负数的性质，求得a，b，c的值，再由勾股定理进行解答即可．
解答：因为a，b，c满足+|a-3|+（b-4）2=0，
所以c-5=0，c=5；
a-3=0，a=3；
b-4=0，b=4，
则32+42=52，即a2+b2=c2，
△ABC的形状是直角三角形．
故选B．
点评：本题考查了非负数的性质．初中阶段有三种类型的非负数：（1）绝对值；（2）偶次方；（3）二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．根据这个结论可以求解这类题目．
分析：利用非负数的性质，求得a，b，c的值，再由勾股定理进行解答即可．
解答：因为a，b，c满足
+|a-3|+（b-4）2=0，所以c-5=0，c=5；
a-3=0，a=3；
b-4=0，b=4，
则32+42=52，即a2+b2=c2，
△ABC的形状是直角三角形．
故选B．
点评：本题考查了非负数的性质．初中阶段有三种类型的非负数：（1）绝对值；（2）偶次方；（3）二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．根据这个结论可以求解这类题目．
练习册系列答案
春雨教育同步作文系列答案
相关题目
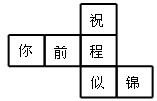35、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示下图是一个正方体的平面展示图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面，则“祝”、“你”、“前”分别表示正方体的
已知函数y=x2+bx+c（x≥0），满足当x=1时，y=-1，且当x=0与x=4时的函数值相等．