题目内容
解方程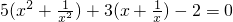
，设
，则原方程可化为关于y的一元二次方程是________．
5y2+3y-12=0
分析：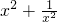
=
-2，则原方程左边=5（y2-2）+3y-2=5y2+3y-12．
解答：设，
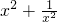∵=-2，
∴原方程左边=5（y2-2）+3y-2=5y2+3y-12．
故原方程可化为关于y的一元二次方程是：5y2+3y-12=0．
点评：本题的关键是把（x2+
）看成一个整体来计算，即用换元法来解题的思想．
分析：
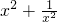=-2，则原方程左边=5（y2-2）+3y-2=5y2+3y-12．解答：设
，∵
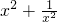=-2，∴原方程左边=5（y2-2）+3y-2=5y2+3y-12．
故原方程可化为关于y的一元二次方程是：5y2+3y-12=0．
点评：本题的关键是把（x2+
）看成一个整体来计算，即用换元法来解题的思想． 
练习册系列答案
相关题目
，设
，则原方程可变形为一元二次方程的一般形式为________．
，设
，则原方程可化为关于y的一元二次方程是 ．
，设
，则原方程可变形为一元二次方程的一般形式为 ．
，设
，则原方程可变形为 ．
，设
，则原方程可变形为 ．