题目内容
17．
如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 设BN=x，则由折叠的性质可得DN=AN=9-x，根据中点的定义可得BD=3，在Rt△BND中，根据勾股定理可得关于x的方程，解方程即可求解．
解答 解：设BN=x，由折叠的性质可得DN=AN=9-x，
∵D是BC的中点，
∴BD=3，
在Rt△NBD中，x2+32=（9-x）2，
解得x=4．
即BN=4．
故选：C．
点评 此题考查了翻折变换（折叠问题），折叠的性质，勾股定理，中点的定义以及方程思想，综合性较强．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
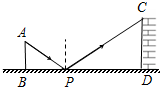如图是孔明设计用手电来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知 AB⊥BD，CD⊥BD，且测得AB=6米，BP=9米，PD=15米，那么该古城墙的高度是（ ）
如图是孔明设计用手电来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知 AB⊥BD，CD⊥BD，且测得AB=6米，BP=9米，PD=15米，那么该古城墙的高度是（ ）| A． | 6米 | B． | 8米 | C． | 10米 | D． | 15米 |
12．
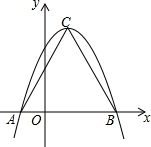如图，二次函数y=-x2+2x+3的图象与x轴交于点A和点B，顶点为C，则sin∠ABC=（ ）
如图，二次函数y=-x2+2x+3的图象与x轴交于点A和点B，顶点为C，则sin∠ABC=（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | 2 | D． | $\frac{1}{2}$ |
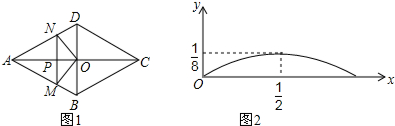
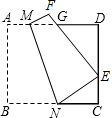如图，将边长为8的正方形纸片ABCD折叠，使点B落在CD边的中点E上，压平后得到折痕MN，EF与AD边交于点G．
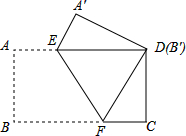把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重叠，折痕为EF，若DF=3，∠FDC=30°，则△DEF的周长是9．