Question

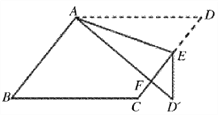
【题目】如图，在矩形中，点在对角线上，过点作，分别交，于点，，连结，.若，，图中阴影部分的面积为，则矩形的周长为_______.

Answer 1

【答案】

【解析】

作PM⊥AD于M，交BC于N，进而得到四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，继而可证明S△PEB=S△PFD，然后根据勾股定理及完全平方公式可求，，进而求出矩形的周长.

解：作PM⊥AD于M，交BC于N，

则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，

∴AM=PE=BN,AE=MP=DF,MD=PF=NC,BE=PN=FC,

S△ADC=S△ABC，S△AMP=S△AEP，S△PBE=S△PBN，S△PFD=S△PDM，S△PFC=S△PCN，

∴S△DFP=S△PBE，且S△DFP+S△PBE=9，

∴，且，

∴，

即，.

∵，，

∴，，

∴，

∴矩形ABCD的周长= 2=.

故答案为：.