题目内容
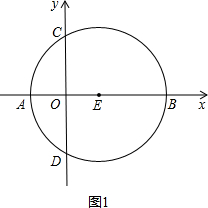
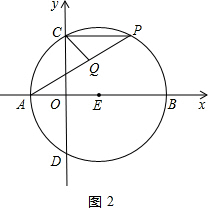
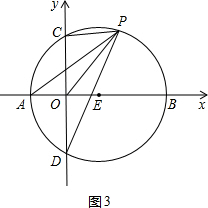
如图，A、B、P是半径为2的⊙O上的三点，∠APB=45°，则弦AB的长为
- A.
- B.2
- C.2
- D.4
C
分析：由A、B、P是半径为2的⊙O上的三点，∠APB=45°，可得△OAB是等腰直角三角形，继而求得答案．
解答：∵A、B、P是半径为2的⊙O上的三点，∠APB=45°，
∴∠AOB=2∠APB=90°，
∴△OAB是等腰直角三角形，
∴AB=OA=2．
故选C．
点评：此题考查了圆周角定理以及等腰直角三角形性质．此题难度不大，注意掌握数形结合思想的应用．
分析：由A、B、P是半径为2的⊙O上的三点，∠APB=45°，可得△OAB是等腰直角三角形，继而求得答案．
解答：∵A、B、P是半径为2的⊙O上的三点，∠APB=45°，
∴∠AOB=2∠APB=90°，
∴△OAB是等腰直角三角形，
∴AB=
OA=2．故选C．
点评：此题考查了圆周角定理以及等腰直角三角形性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
的坐标是（1，0）
（2013•重庆）如图，菱形OABC的顶点O是坐标原点，顶点A在x轴的正半轴上，顶点B、C均在第一象限，OA=2，∠AOC=60°．点D在边AB上，将四边形OABC沿直线0D翻折，使点B和点C分别落在这个坐标平面的点B′和C′处，且∠C′DB′=60°．若某反比例函数的图象经过点B′，则这个反比例函数的解析式为