题目内容
 如图,已知AB∥DE,AB=DE,请你添加一个条件
如图,已知AB∥DE,AB=DE,请你添加一个条件∠A=∠D
∠A=∠D
,可以根据“ASA”得△ABC≌△DEF;或者添加条件BE=CF,可以根据SAS
SAS
得到△ABC≌△DEF.分析:①添加∠A=∠D,首先根据AB∥DE可得∠B=∠DEF,然后根据ASA证明△ABC≌△DEF;
②由BE=CF可得BC=EF,再利用SAS可证明△ABC≌△DEF.
②由BE=CF可得BC=EF,再利用SAS可证明△ABC≌△DEF.
解答:解:①添加∠A=∠D,
∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA);
故答案为:∠A=∠D;
②∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
故答案为:SAS.
∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(ASA);
故答案为:∠A=∠D;
②∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS).
故答案为:SAS.
点评:此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( )
5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( ) 如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上,
如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上, 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
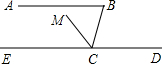 如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.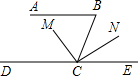 如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.