题目内容
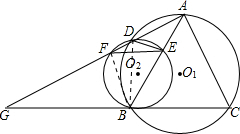
已知，如图，△ABC内接于⊙O1，AB=AC，⊙O2与BC相切于点B，与AB相交于点E，与⊙O1相交于点D，直线AD交⊙O2于点F，交CB的延长线于点G．
求证：（1）∠G=∠AFE；（2）AB•EB=DE•AG．
求证：（1）∠G=∠AFE；（2）AB•EB=DE•AG．
证明：（1）连接BD．
∵∠FEB=∠FDB，∠FDB=∠C，
∴∠FEB=∠C．
又∵AB=AC，
∴∠ABC=∠C．
∴∠FEB=∠ABC．
∴EF∥CG．
∴∠G=∠AFE．
（2）连接BF．
∵∠ADE=∠ABF，∠DAE=∠BAF，
∴△ADE∽△ABF．
∴
=
．
又∵EF∥CG，
∴
=
即
=
．
∵∠BEF=∠ABC，∠ABC=∠BFE，
∴∠BEF=∠BFE．
∴BE=BF．
∴
=
，即AB•EB=DE•AG．
∵∠FEB=∠FDB，∠FDB=∠C，
∴∠FEB=∠C．
又∵AB=AC，
∴∠ABC=∠C．
∴∠FEB=∠ABC．
∴EF∥CG．
∴∠G=∠AFE．
（2）连接BF．
∵∠ADE=∠ABF，∠DAE=∠BAF，
∴△ADE∽△ABF．
∴
| DE |
| BF |
| AE |
| AF |
又∵EF∥CG，
∴
| AE |
| AF |
| AB |
| AG |
| DF |
| BF |
| AB |
| AG |
∵∠BEF=∠ABC，∠ABC=∠BFE，
∴∠BEF=∠BFE．
∴BE=BF．
∴
| DE |
| BE |
| AB |
| AG |
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
B=2∠PCB．
