题目内容
17.先化简,再求值:$({\frac{1}{x+2}+\frac{2}{{{x^2}-4}}})÷\frac{x^2}{x+2}$,其中x2-2x-3=0.分析 首先把括号内的式子通分相加,把除法转化为乘法,计算乘法即可化简,然后把x2-2x-3=0化成x2-2x=3的形式,代入求值即可.
解答 解:原式=$[{\frac{1}{x+2}+\frac{2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$[{\frac{x-2}{{({x+2})({x-2})}}+\frac{2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$[{\frac{x-2+2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$\frac{x}{{({x+2})({x-2})}}÷\frac{x^2}{x+2}$
=$\frac{x}{{({x+2})({x-2})}}•\frac{x+2}{x^2}$
=$\frac{1}{{x({x-2})}}$.
∵x2-2x-3=0
∴x2-2x=3,
∴原式=$\frac{1}{3}$.
点评 本题考查了分式的化简求值,正确对所求的分式进行通分、约分,正确进行化简是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.不等式(1-a) x>2变形后得到$x<\frac{2}{1-a}$成立,则a的取值( )
| A. | a>0 | B. | a<0 | C. | a>1 | D. | a<1 |
9.甲看乙是南偏东47°,则乙看甲的方向是( )
| A. | 南偏西47° | B. | 北偏西47° | C. | 北偏西43° | D. | 西偏北47° |
7.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
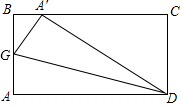 如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度. 已知:如图∠B=40°,∠B=∠BAD,∠C=∠ADC,则∠DAC的度数为20°.
已知:如图∠B=40°,∠B=∠BAD,∠C=∠ADC,则∠DAC的度数为20°.