题目内容
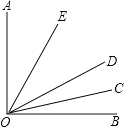
【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
【答案】(1)∠EOC=45°;(2)∠EOC=![]() α;(3)∠EOC=70°.
α;(3)∠EOC=70°.
【解析】
(1)根据角平分线的定义以及角的和差定义计算即可;
(2)利用(1)中结论计算即可;
(3)分别求出∠EOD,∠DOC即可解决问题.
解:(1)∵OE平分∠AOD,OC平分∠BOD,
∴∠EOD=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB,
∠DOB,
∴∠EOC=![]() (∠AOD+∠DOB)=45°;
(∠AOD+∠DOB)=45°;
(2)由(1)可知:∠EOC=![]() (∠AOD+∠DOB)=
(∠AOD+∠DOB)=![]() α;
α;
(3)∵∠DOE:∠DOC=4:3,
∴设∠DOE=4x,∠DOC=3x,
∵∠EOA=![]() ∠AOD,
∠AOD,
∴∠DOE=![]() ∠AOD,
∠AOD,
∴∠AOD=5x,
∵∠DOC=![]() ∠DOB,
∠DOB,
∴∠DOB=4x,
∵∠AOB=90°,
∴5x+4x=90°,
∴x=10°,
∴∠EOC=∠EOD+∠DOC=7x=70°.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目