Question

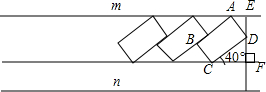
某住宅小区的物业管理部门为解决住户停车困难，将一条道路辟为停车场，停车位置如图所示。已知矩形ABCD是供一辆机动车停放的车位，其中AB=5.4米，BC=2.2米，。请计算停车位所占道路的宽度EF（结果精确到0.1米）。

参考数据：sin40°≈0.64   cos40°≈0.77   tan40°≈0.84

 

Answer 1

【答案】

5.2米

【解析】由题意知∠DFC = 90°，∠DEA = 90°∠DCF = 40°

    又∵ABCD是矩形

∴AB = CD = 5.4 米   BC = AD = 2.2米 且∠ADC = 90°…………………1分

∵∠DCF + ∠CDF = 90°且∠ADE + ∠CDF = 90°

∴∠DCF =∠ADE = 40°…………………………………………………………1分

在Rt△DCF中，sin∠DCF =  

 DF = CD sin∠DCF=5.4×sin40°≈5.4×0.64=3.456………1分

在Rt△DAE中，COS∠ADE =  

 DE = AD cos∠ADE=2.2×cos40°≈2.2×0.77=1.694………1分

        EF=DE+DF ≈3.456+1.694=5.2………………………………………………1分

     ∴停车位所占道路宽度EF约为5.2米。…………………………………………1分

在直角三角形中，利用三角函数关系，有已知角度和边求得ED和DF，而求得EF的长．