Question

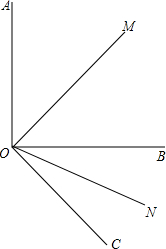如图所示，已知∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC．
（1）∠MON=______；
（2）如果∠AOB=α，∠BOC=β，其它条件不变，那么∠MON=______ （用含α，β的式子表示）；
（3）若将条件变成O是直线AC上一点，OB为一条射线，OM平分∠AOB，ON平分∠BOC，请你猜想一个结论，并说明它是正确的．

Answer 1

解（1）∵∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，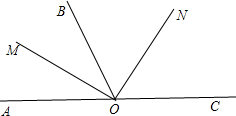
∴∠BOM=∠AOB=45°，∠NOB=∠BOC=15°，
∴∠MON=∠BOM+∠BON=60°；

（2）∵∠BOM=∠AOB=α，∠NOB=∠BOC=β，
∴∠MON=∠BOM+∠BON=α+β=（α+β）；

（3）∠MON=90°．理由如下：
∵O是直线AC上一点，
∴∠AOC=180°，
∵OM平分∠AOB，ON平分∠BOC，
∴∠BOM=∠AOB，∠NOB=∠BOC，
∴∠MON=∠BOM+∠BON=（∠AOB+∠BOC）=∠AOC=90°．
分析：（1）根据角平分线的定义得到∠BOM=∠AOB=45°，∠NOB=∠BOC=15°，则∠MON=∠BOM+∠BON=60°；
（2）同理得到∠BOM=∠AOB=α，∠NOB=∠BOC=β，则∠MON=∠BOM+∠BON=α+β=（α+β）；
（3）由O是直线AC上一点得到∠AOC=180°，根据角平分线的定义得到∠BOM=∠AOB，∠NOB=∠BOC，所以∠MON=∠BOM+∠BON=（∠AOB+∠BOC）=∠AOC．
点评：本题考查了角度的计算：∠AOB是∠AOC和∠BOC的和，记作：∠AOB=∠AOC+∠BOC；∠AOC是∠AOB和∠BOC的差，记作：∠AOC=∠AOB-∠BOC．