题目内容
如图①,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F。
(1)如图②,当BP=BA时,∠EBF= ,猜想∠QFC= ;(2分)
(2)如图①,当点P为射线BC上任意一点时,求证∠QFC=60°;(4分)
 (3)已知线段AB=
(3)已知线段AB=![]() ,设BP=
,设BP=![]() ,点Q到射线BC的距离为
,点Q到射线BC的距离为![]() ,求
,求![]() 关于
关于![]() 的函数关系式。(4分)
的函数关系式。(4分)
 |
 解:(1)
解:(1)![]() 30°...............................1分
30°...............................1分
![]() = 60°..................................1分
= 60°..................................1分
(2)不妨设BP>![]() , 如图1所示
, 如图1所示
∵∠BAP=∠BAE+∠EAP=60°+∠EAP
∠EAQ=∠QAP+∠EAP=60°+∠EAP
∴∠BAP=∠EAQ..........................................2分
 在△ABP和△AEQ中 AB=AE,∠BAP=∠EAQ, AP=AQ
在△ABP和△AEQ中 AB=AE,∠BAP=∠EAQ, AP=AQ
∴△ABP≌△AEQ(SAS)
∴∠AEQ=∠ABP=90°...............................3分
∴∠BEF![]()
∴![]() =
=![]()
![]() 60°……………............4分
60°……………............4分
(事实上当BP≤![]() 时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)
时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)
(3)在图1中,过点F作FG⊥BE于点G
∵△ABE是等边三角形 ∴BE=AB=![]() ,由(1)得
,由(1)得![]() 30°
30°
在Rt△BGF中,![]() ∴BF=EF=2 .......1分
∴BF=EF=2 .......1分
∵△ABP≌△AEQ ∴QE=BP=![]() ∴QF=QE+EF
∴QF=QE+EF![]() ................2分
................2分
过点Q作QH⊥BC,垂足为H,
在Rt△QHF中,![]() 60°,
60°,
∴![]() (x>0)
(x>0)
即y关于x的函数关系式是:![]() .......................................................4分
.......................................................4分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案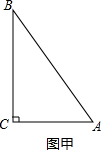 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.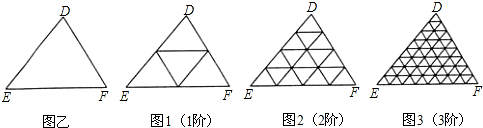
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

