题目内容
已知
-
=8,求x的取值范围.
| (x-3)2 |
| (x+5)2 |
考点:二次根式的性质与化简
专题:
分析:根据题意得出x-3<0,x+5<0,进而得出x的取值范围.
解答:解:∵
-
=8,
只有3-x+x+5=8,
∴x-3<0,x+5<0,
解得:x<-5.
故x的取值范围是:x<-5.
| (x-3)2 |
| (x+5)2 |
只有3-x+x+5=8,
∴x-3<0,x+5<0,
解得:x<-5.
故x的取值范围是:x<-5.
点评:此题主要考查了二次根式的性质与化简,正确得出根号下各项符号是解题关键.

练习册系列答案
相关题目
某服装店在进一批服装时,进价已按原价打了七五折,商店打算对该批服装定一新价标在价目卡上,并注明按标价降价20%销售,这样仍可获得25%的纯利润,求服装店给这批服装定的新标价y与原价x之间的函数关系 .
若|a|=4,
=3,且|a+b|=-a-b,则a-b的值是( )
| b2 |
| A、1或7 | B、-1或-7 |
| C、-1或7 | D、1或-7 |
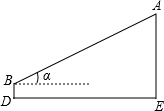 如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为
如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为 如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.
如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.