��Ŀ����
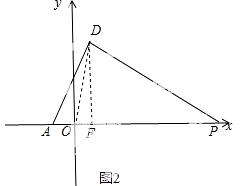
��ͼ��������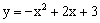 ��x���ཻ��A��B���㣬��y�ύ��C������ΪD�������ߵĶԳ���DF��BC�ཻ�ڵ�E����x���ཻ�ڵ�F��
��x���ཻ��A��B���㣬��y�ύ��C������ΪD�������ߵĶԳ���DF��BC�ཻ�ڵ�E����x���ཻ�ڵ�F��
��1�����߶�DE�ij���
��2�����E��ֱ�����������ཻ��M��x1��y1����N��x2��y2�������жϵ�|x1﹣x2|��ֵ��Сʱ��ֱ��MN��x���λ�ù�ϵ����˵�����ɣ�
��3����PΪx���ϵ�һ�㣬��DAO+��DPO=�Ϧ�����tan�Ϧ�=4ʱ�����P�����꣮
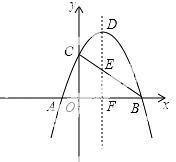

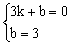 �����
�����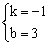 .
.

��x1+x2=b1��x1x2=b1﹣3.
��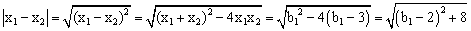 ��
��
�൱b1=2ʱ��|x1﹣x2|��Сֵ=2 .
.
��b1=2ʱ��y=��2﹣b1��x+b1=2����ֱ��MN��x�ᣮ
��3�����ͼ����D��1��4������tan��DOF=4.
�֡�tan�Ϧ�=4�����DOF=�Ϧ�.
�ߡ�DOF=��DAO+��ADO=�Ϧ��� ��DAO+��DPO=�Ϧ������DPO=��ADO.
��DAO+��DPO=�Ϧ������DPO=��ADO.
���ADP�ס�AOD. ��AD2=AO•AP.
��AF=2��DF=4��
��AD2=AF2+DF2=20. ��OP=19.
��P1��19��0����P2�� ﹣17��0����
﹣17��0����

����ʽ����ȷ���ǣ�������
| �� | A�� | ��a��b��2=a2��2ab+b2 | B�� | ��a��b��2=a2��b2 | C�� | ��a��b��2=a2+2ab+b2 | D�� | ��a��b��2=a2��ab+b2 |
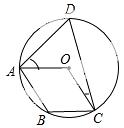
��֪��A������Ϊ��2��0������P��ֱ��y=x���˶������Ե�PΪԲ�ģ�PA�ij�Ϊ�뾶��Բ�������Сʱ����P������Ϊ��������
| �� | A�� | ��1����1�� | B�� | ��0��0�� | C�� | ��1��1�� | D�� | �� |

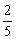 �����������ٷ�
�����������ٷ� ��1��������ʱȡ�ú���ĸ��ʱ�Ϊ
��1��������ʱȡ�ú���ĸ��ʱ�Ϊ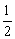 ��
�� ��
��
 �պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
�պó鵽ͬ�Ա�ѧ���ĸ��ʣ�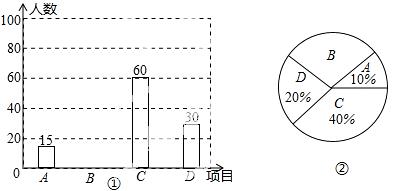 ��
��