题目内容
如图，AD是∠CAE的平分线，∠B=29°，∠ACD=99°，那么∠DAE等于
- A.55°
- B.59°
- C.45°
- D.49°
A
分析：根据角平分线的性质及三角形内角和定理解答．
解答：∵∠B=29°，∠ACD=99°，∴∠ACB=180°-∠ACD=180-99°=81°，
∴∠CAE=∠B+∠ACB=29°+81°=110°．
∴∠DAE=
∠CAE=55°．
故选A．
点评：此题主要考查角平分线的性质、三角形外角的性质和平角的定义．
分析：根据角平分线的性质及三角形内角和定理解答．
解答：∵∠B=29°，∠ACD=99°，∴∠ACB=180°-∠ACD=180-99°=81°，
∴∠CAE=∠B+∠ACB=29°+81°=110°．
∴∠DAE=
∠CAE=55°．故选A．
点评：此题主要考查角平分线的性质、三角形外角的性质和平角的定义．
练习册系列答案
相关题目
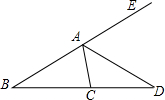如图，AD是∠CAE的平分线，∠B=29°，∠ACD=99°，那么∠DAE等于（ ）| A、55° | B、59° | C、45° | D、49° |
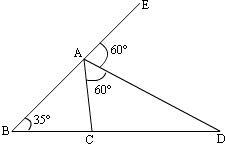
如图，AD是∠CAE的平分线，∠B=45°，∠DAE=75°，则∠ACD为（ ）
如图，AD是∠CAE的平分线，∠B=35°，∠DAE=60°，那么∠ACB等于（ ）