题目内容
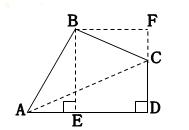
如图,四边形ABCD中,∠ABC=90°,CD⊥AD,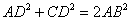 ,
,
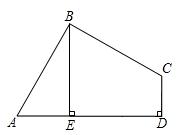
(1)求证:AB=BC;
(2)过点B作BE⊥AD于E,若四边形ABCD的面积为 ,求BE的长.
,求BE的长.
(1)连接AC ,由勾股定理得
,由勾股定理得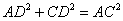 ,
,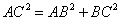 ,又
,又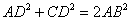 ,所以
,所以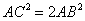 ,所以
,所以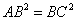 ,所以AB=BC.
,所以AB=BC.
(2)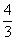 .
.
【解析】
试题分析:(1)连接AC,由勾股定理得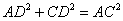 ,又
,又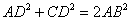 ,所以
,所以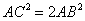 ,所以
,所以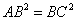 ,问题得证;
,问题得证;
(2)过点B作BF⊥BE,延长DC交BF于F,即可证得△ABE≌△CBF,则S四边形BEDF=S四边形ABCD= ,又四边形BEDF为正方形,则BE=
,又四边形BEDF为正方形,则BE=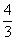 .
.
试题解析:(1)连接AC,由勾股定理得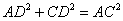 ,
,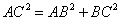 ,又
,又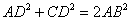 ,所以
,所以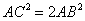 ,所以
,所以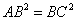 ,所以AB=BC.
,所以AB=BC.
(2)过点B作BF⊥BE,延长DC交BF于F,因为∠AEB=∠F,∠ABE=∠CBF,AB=BC,所以△ABE≌△CBF,所以BF=BE, 四边形BEDF为正方形,则S四边形BEDF=S四边形ABCD= ,又四边形BEDF为正方形,所以BE=
,又四边形BEDF为正方形,所以BE=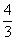 .
.
【难度】一般

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图:
甲、乙射击成绩统计表
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 0 | ||
| 乙 | 1 |


(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
 是匀速行走,且下山比上山时的速度每小时快1千米,求小张上山时的速度.
是匀速行走,且下山比上山时的速度每小时快1千米,求小张上山时的速度.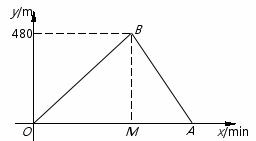
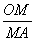 = ;
= ; (即贷款).
(即贷款).


 ,其中
,其中 ,
, .
. 与直线
与直线 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于
 的不等式
的不等式 的解集为 .
的解集为 .
