题目内容
下列结论正确的是( )
分析:根据分式有意义,分母不等于0;分式的值等于0,分子等于0,分母不等于0对各选项分析判断后利用排除法求解.
解答:解:A、分式有意义,3x-2≠0,解得x≠
,故本选项正确;
B、分式有意义,x2-y2≠0,解得x≠±y,故本选项错误;
C、分式的值等于0,x=0且x2+2x≠0,解得x=0且x≠0或-2,所以,分式的值不等于0,故本选项错误;
D、分式没有意义,x-1=0,x=1,故本选项错误.
故选A.
| 2 |
| 3 |
B、分式有意义,x2-y2≠0,解得x≠±y,故本选项错误;
C、分式的值等于0,x=0且x2+2x≠0,解得x=0且x≠0或-2,所以,分式的值不等于0,故本选项错误;
D、分式没有意义,x-1=0,x=1,故本选项错误.
故选A.
点评:本题考查了分式有意义以及分式的值为零的条件,从以下三个方面透彻理解分式的概念:
(1)分式无意义?分母为零;
(2)分式有意义?分母不为零;
(3)分式值为零?分子为零且分母不为零.
(1)分式无意义?分母为零;
(2)分式有意义?分母不为零;
(3)分式值为零?分子为零且分母不为零.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下列结论正确的是( )
A、
| ||
B、当x=-3时,分式
| ||
| C、(-a+b)(-a-b)=a2-b2 | ||
| D、a2+a3=a5 |
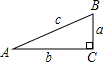 如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )
如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )A、sinB=
| ||
B、cosB=
| ||
C、tanB=
| ||
D、cotB=
|
如果-b是a的立方根(ab≠0),那么下列结论正确的是( )
| A、-b也是-a的立方根 | B、b是a的立方根 | C、b是-a的立方根 | D、以上结论均不正确 |
