ĢāÄæÄŚČŻ
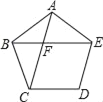
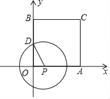
”¾ĢāÄæ”æij¹«Ō°ŌŚŅ»øöÉČŠĪOEF²ŻĘŗÉĻµÄŌ²ŠÄO“¦“¹Ö±ÓŚ²ŻĘŗµÄµŲÉĻŹśŅ»øłÖł×ÓOA£¬ŌŚA“¦°²×°Ņ»øö×Ō¶ÆÅēĖ®×°ÖĆ£®ÅēĶ·ĻņĶāÅēĖ®£®Į¬ÅēĶ·ŌŚÄŚ£¬Öłøß![]() m£¬Ė®Į÷ŌŚø÷øö·½ĻņÉĻŃŲŠĪדĻąĶ¬µÄÅ×ĪļĻßĀ·¾¶ĀäĻĀ£¬Åē³öµÄĖ®Į÷ŌŚÓėDµćµÄĖ®Ę½¾ąĄė4Ćד¦“ļµ½×īøßµćB£¬µćB¾ąĄėµŲĆę2Ć×£®µ±ÅēĶ·AŠż×Ŗ120”揱£¬Õāøö²ŻĘŗæÉŅŌČ«±»Ė®ø²øĒ£®ČēĶ¼1ĖłŹ¾£®
m£¬Ė®Į÷ŌŚø÷øö·½ĻņÉĻŃŲŠĪדĻąĶ¬µÄÅ×ĪļĻßĀ·¾¶ĀäĻĀ£¬Åē³öµÄĖ®Į÷ŌŚÓėDµćµÄĖ®Ę½¾ąĄė4Ćד¦“ļµ½×īøßµćB£¬µćB¾ąĄėµŲĆę2Ć×£®µ±ÅēĶ·AŠż×Ŗ120”揱£¬Õāøö²ŻĘŗæÉŅŌČ«±»Ė®ø²øĒ£®ČēĶ¼1ĖłŹ¾£®
£Ø1£©½ØĮ¢ŹŹµ±µÄ×ų±źĻµ£¬Ź¹AµćµÄ×ų±źĪŖ£ØO£¬![]() £©£¬Ė®Į÷µÄ×īøßµćBµÄ×ų±źĪŖ£Ø4£¬2£©£¬Ēó³ö“Ė×ų±źĻµÖŠÅ×ĪļĻßĖ®Į÷¶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½£»
£©£¬Ė®Į÷µÄ×īøßµćBµÄ×ų±źĪŖ£Ø4£¬2£©£¬Ēó³ö“Ė×ų±źĻµÖŠÅ×ĪļĻßĖ®Į÷¶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ĒóÅēĖ®×°ÖĆÄÜÅē¹ąµÄ²ŻĘŗµÄĆ껿£Ø½į¹ūÓƦŠ±ķŹ¾£©£»
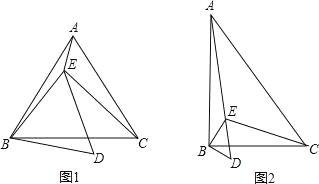
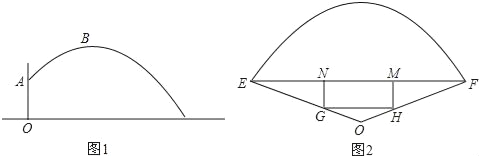
£Ø3£©ŌŚÉČŠĪOEFµÄŅ»æéČż½ĒŠĪĒųÓņµŲæé”÷OEFÖŠ£¬ĻÖŅŖ½ØŌģŅ»øö¾ŲŠĪGHMN»ØĢ³£¬ČēĶ¼2µÄÉč¼Ę·½°øŹĒŹ¹H”¢G·Ö±šŌŚOF”¢OEÉĻ£¬MNŌŚEFÉĻ£®ÉčMN£½2x£¬µ±xČ”ŗĪÖµŹ±£¬¾ŲŠĪGHMN»ØĢ³µÄĆ껿×ī“ó£æ×ī“óĆ껿ŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©y£½©![]() £Øx©4£©2+2£»£Ø2£©
£Øx©4£©2+2£»£Ø2£©![]() £ØĘ½·½Ć×£©£»£Ø3£©µ±x=
£ØĘ½·½Ć×£©£»£Ø3£©µ±x=![]() Ź±£¬SµÄÖµ×ī“óĪŖ£ŗ
Ź±£¬SµÄÖµ×ī“óĪŖ£ŗ![]() £ØĘ½·½Ć×£©£®
£ØĘ½·½Ć×£©£®
”¾½āĪö”æ
£Ø1£©ĄūÓƶ„µćŹ½Ēó³ö¶ž“ĪŗÆŹż½āĪöŹ½¼“æÉ£»
£Ø2£©ĄūÓĆy£½0Ź±Ēó³öĶ¼ĻóÓėxÖįµÄ½»µć×ų±ź£¬½ų¶ųµĆ³öÉČŠĪµÄ°ė¾¶£¬¼“æÉµĆ³öSµÄÖµ£»
£Ø3£©ĄūÓĆČń½ĒČż½ĒŗÆŹż¹ŲĻµµĆ³öMHµÄ³¤£¬ŌŁĄūÓƶž“ĪŗÆŹż×īÖµ¹«Ź½Ēó³ö¼“æÉ£®
£Ø1£©øł¾ŻĢāŅāµĆ³ö£ŗĶ¼Ļ󶄵ć×ų±źĪŖ£ŗ£Ø4£¬2£©£¬
¹ŹÉč½āĪöŹ½ĪŖ£ŗy£½a£Øx©4£©2+2£¬
½«£Ø0£¬![]() £©£¬“śČėÉĻŹ½µĆ£ŗ
£©£¬“śČėÉĻŹ½µĆ£ŗ
![]() £½a£Ø0©4£©2+2£¬
£½a£Ø0©4£©2+2£¬
½āµĆ£ŗa£½©![]() £¬
£¬
”ąÅ×ĪļĻßĖ®Į÷¶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗy£½©![]() £Øx©4£©2+2£»
£Øx©4£©2+2£»
£Ø2£©µ±y£½0Ź±£¬
0£½©![]() £Øx©4£©2+2£¬
£Øx©4£©2+2£¬
½āµĆ£ŗx1£½10£¬x2£½©2£ØÉįČ„£©£¬
”ąÉČŠĪ°ė¾¶ĪŖ10Ć×£¬
”ąS£½![]() £ØĘ½·½Ć×£©£»
£ØĘ½·½Ć×£©£»
£Ø3£©¹żµćO×÷OA”ĶEFÓŚµćA£¬½»GHÓŚµćB£¬
”ß”ĻEOF£½120”ć£¬EO£½FO£½10£¬
”ą”ĻOEF£½”ĻOFE£½30”ć£¬
”ąAO£½![]() FO£½5£¬
FO£½5£¬
ÉčMN£½2x£¬
”ąAM£½BH£½x£¬
”ąBO£½![]() x£¬
x£¬
”ąMH£½5©![]() x£¬
x£¬
ÓÉĢāŅāµĆ³ö£ŗ
S£½2x£Ø5©![]() x£©£½©
x£©£½©![]() x2©10x£¬
x2©10x£¬
µ±x£½©![]() £½
£½![]()
![]() Ź±£¬
Ź±£¬
SµÄÖµ×ī“óĪŖ£ŗS£½![]()
![]() £ØĘ½·½Ć×£©£®
£ØĘ½·½Ć×£©£®

 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø