题目内容
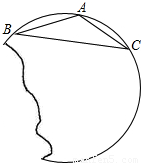
 如图,要把破残的圆片复制完整,已知弧上的三点A、B、C,
如图,要把破残的圆片复制完整,已知弧上的三点A、B、C,(1)用尺规作图法,找出弧ABC所在圆的圆心O(保留作图痕迹,不写作法);
(2)设△ABC是等腰三角形,底边BC=10cm,腰AB=6cm,求圆片的半径R(结果保留根号);
(3)若在(2)题中的R的值满足n<R<m(m、n为正整数),试估算m和n的值.
分析:(1)作出AB,BC的中垂线,交点即为圆心O;
(2)连接OA,设与BC交于点D,并延长AD,连接OB,由△ABC是等腰三角形,推出DB=DC,根据垂径定理确定AD的延长线过O点,再由AB=AC=6cm,BC=10cm,根据勾股定理推出AD=
cm,由R2=52+(R-
)2,即可求出R的值;
(3)由
≈3.3166,推出R=
≈5.4272,根据n<R<m(m、n为正整数),推出n可取的最大值为5,m可取的最小值为6,即可估算出n=5,m=6.
(2)连接OA,设与BC交于点D,并延长AD,连接OB,由△ABC是等腰三角形,推出DB=DC,根据垂径定理确定AD的延长线过O点,再由AB=AC=6cm,BC=10cm,根据勾股定理推出AD=
| 11 |
| 11 |
(3)由
| 11 |
18
| ||
| 11 |
解答:解:(1)

(2)作AD⊥BC于D,并延长AD,连接OB,
∵△ABC是等腰三角形,
∴DB=DC,
∴AD的延长线过O点,
∵AB=AC=6cm,BC=10cm,
∴BD=5cm,
∴AD=
cm,
∵OB=OA=R,
∴R2=52+(R-
)2,
∴R=
,

(3)∵
≈3.3166,
∴R=
≈5.4272,
∵n<R<m(m、n为正整数),
∴n可取的最大值为5,m可取的最小值为6,
∴n=5,m=6.

(2)作AD⊥BC于D,并延长AD,连接OB,
∵△ABC是等腰三角形,
∴DB=DC,
∴AD的延长线过O点,
∵AB=AC=6cm,BC=10cm,
∴BD=5cm,
∴AD=
| 11 |
∵OB=OA=R,
∴R2=52+(R-
| 11 |
∴R=
18
| ||
| 11 |

(3)∵
| 11 |
∴R=
18
| ||
| 11 |
∵n<R<m(m、n为正整数),
∴n可取的最大值为5,m可取的最小值为6,
∴n=5,m=6.
点评:本题主要考查垂径定理,勾股定理等性质定理,关键在于熟练运用各性质定理,正确的画出辅助线,认真的进行计算.

练习册系列答案
相关题目
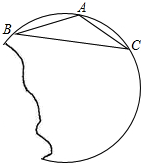 如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
 如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
如图,要把破残的圆片复制完整,已知弧上的点A、B、C. 所在圆的圆心O;
所在圆的圆心O;
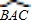 所在圆的圆心O;
所在圆的圆心O;