��Ŀ����
14��ij��ˮ�ص���ˮ��ÿСʱ��ˮ8m3��6Сʱ�ɽ�����ˮȫ���ſգ���1����ˮ�ص��ݻ���48 m3��
��2�����������ˮ�ܣ�ʹÿСʱ��ˮ���ﵽQ��m3������ô������ˮ�ſ�����ʱ��Ϊt��Сʱ������Q��t֮���ϵʽΪQ=$\frac{48}{t}$��
��3���������5Сʱ�ڽ�����ˮ�ſգ���ôÿСʱ����ˮ������Ϊ9.6 m3/Сʱ��
��4����֪��ˮ�����ΪÿСʱ12m3��������4Сʱ�ɽ�����ˮȫ���ſգ�
���� ��1��������ˮ��ÿСʱ��ˮ8m3��6Сʱ�ɽ�����ˮȫ���ſռ��ɵó���ˮ�ص��ݻ���
��2�����ã�1��������ó�Q��t�ĺ�����ϵʽ��
��3�����ã�2���ĺ�����ϵʽ�ó�ÿСʱ����ˮ����
��4�����ã�2���ĺ�����ϵʽ����Q=12���룬�ó��𰸣�
��� �⣺��1������ˮ�ص���ˮ��ÿСʱ��ˮ8m3��6Сʱ�ɽ�����ˮȫ���ſգ�
����ˮ�ص��ݻ��ǣ�6��8=48��m3����
�ʴ�Ϊ��48��
��2����������ˮ�ܣ�ʹÿСʱ��ˮ���ﵽQ��m3����������ˮ�ſ�����ʱ��Ϊt��Сʱ����
��Q��t֮���ϵʽΪ��Q=$\frac{48}{t}$��
�ʴ�Ϊ��Q=$\frac{48}{t}$��
��3��������5Сʱ�ڽ�����ˮ�ſգ�
��ÿСʱ����ˮ������Ϊ��$\frac{48}{5}$=9.6��m3����
�ʴ�Ϊ��9.6��
��4������ˮ�����ΪÿСʱ12m3��
��$\frac{48}{t}$=12��
��ã�t=4��
������4Сʱ�ɽ�����ˮȫ���ſգ�
�ʴ�Ϊ��4��
���� ������Ҫ�����˷�����������Ӧ�ã����������ҵ���ȷ������ϵ�ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
4�����и�ʽ������ȷ���ǣ�������
| A�� | 2$+\sqrt{2}$=2$\sqrt{2}$ | B�� | 3$\sqrt{3}$-$\sqrt{2}$=2$\sqrt{2}$ | C�� | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}$-$\sqrt{5}$ | D�� | 2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$=3$\sqrt{2}$-2$\sqrt{3}$ |
5������ȥ������ȷ���ǣ�������
| A�� | a-��b+c��=a-b+c | B�� | a-��b-c��=a-b-c | C�� | a-��-b+c��=a+b+c | D�� | a-��-b-c��=a+b+c |
2������˵����ȷ���ǣ�������
| A�� | �ܹ���ȫ�غϵ�����ͼ�ν���ȫ��ͼ�� | |
| B�� | �ܳ���ȵ���������ȫ�������� | |
| C�� | ������ȵ���������ȫ�������� | |
| D�� | �����ȵ���������ȫ�������� |
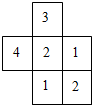 һ���������ɴ�С��ͬ��С��������ɣ������濴���ļ��������״��ͼ��ʾ������С�����������ֱ�ʾ��λ�õ�С������ĸ������뻭��������ʹ����濴����������������״ͼ��
һ���������ɴ�С��ͬ��С��������ɣ������濴���ļ��������״��ͼ��ʾ������С�����������ֱ�ʾ��λ�õ�С������ĸ������뻭��������ʹ����濴����������������״ͼ��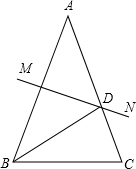 ��ͼ��������ABC�У�AB=AC����A=40�ȣ�AB�Ĵ�ֱƽ����MN��AC��D������BD����DBC����30�ȣ�
��ͼ��������ABC�У�AB=AC����A=40�ȣ�AB�Ĵ�ֱƽ����MN��AC��D������BD����DBC����30�ȣ�