题目内容
 如图平行四边形ABCD中,∠ABD=30°,AB=4,AE⊥BD,CF⊥BD,且,E,F恰好是BD的三等分点,又M、N分别是AB,CD的中点,那么四边形MENF的面积是
如图平行四边形ABCD中,∠ABD=30°,AB=4,AE⊥BD,CF⊥BD,且,E,F恰好是BD的三等分点,又M、N分别是AB,CD的中点,那么四边形MENF的面积是| 3 |
| 3 |
分析:由已知条件可得MF与EF的长,进而可得Rt△MEF的面积,即可求解四边形MENF的面积.
解答:解:∵E,F为BD的三等分点,
∴BF=EF.又AM=BM,
∴MF是△ABE的中位线.MF=
AE=1.
又EF=
BE=
,MF⊥BE,
∴S△MEF=
,
∴SMENF=2S△MEF=
.
∴BF=EF.又AM=BM,
∴MF是△ABE的中位线.MF=
| 1 |
| 2 |
又EF=
| 1 |
| 2 |
| 3 |
∴S△MEF=
| ||
| 2 |
∴SMENF=2S△MEF=
| 3 |
点评:本题主要考查了平行四边形的性质以及三角形中位线定理,能够利用其性质求解一些简单的计算问题.

练习册系列答案
相关题目
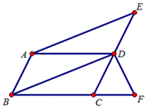 24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2
24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
 为点F,DF=2
为点F,DF=2 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,