题目内容
△ABC中,∠ACB=90°,AB=4,⊙C的半径长是2,当∠A=30°时,⊙C与直线AB的位置关系是________;当∠A=45°时,⊙C与直线AB的位置关系是________.
相交 相切
分析:据题意画出相应的图形,然后过C作CD与AB垂直,垂足为D,在直角三角形ACD中,由30°角所对的直角边等于斜边的一半,由斜边AB的长和面积定值求出CD的长,即为圆心到直线的距离,小于圆C的半径,可得圆C与直线AB相交;当∠A=45°时,求出CD的长和圆的半径2比较大小即可.
解答:根据题意画出图形,如图所示:
当∠A=30°,
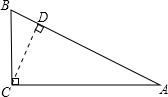
过C作CD⊥AB,交AB于点D.
在Rt△ACD中,∵AB=4,∠A=30°,
∴BC= AB=2,
AB=2,
∴AC=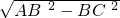 =2
=2 ,
,
∴CD= AC=
AC= ,
,
又∵圆C的半径为2,则 <2,
<2,
∴CD<R,
∴则⊙C与AB的位置关系是相交;
故答案为:相交;
当∠A=45°时,
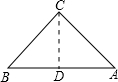
过C作CD⊥AB,交AB于点D.
在Rt△ACD中,∵AB=4,∠A=45°,
∴AB=AC,
∴CD= AB=2,
AB=2,
又∵圆C的半径为2,则CD=R,
∴则⊙C与AB的位置关系是相切.
故答案为:相切.
点评:此题考查了直线与圆的位置关系,以及直角三角形的性质,直线与圆的位置关系有三种,分别为相切,相交,相离,可以利用d与r比较大小来决定,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当0≤d<r时,直线与圆相交.
分析:据题意画出相应的图形,然后过C作CD与AB垂直,垂足为D,在直角三角形ACD中,由30°角所对的直角边等于斜边的一半,由斜边AB的长和面积定值求出CD的长,即为圆心到直线的距离,小于圆C的半径,可得圆C与直线AB相交;当∠A=45°时,求出CD的长和圆的半径2比较大小即可.
解答:根据题意画出图形,如图所示:
当∠A=30°,

过C作CD⊥AB,交AB于点D.
在Rt△ACD中,∵AB=4,∠A=30°,
∴BC=
 AB=2,
AB=2,∴AC=
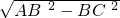 =2
=2 ,
,∴CD=
 AC=
AC= ,
,又∵圆C的半径为2,则
 <2,
<2,∴CD<R,
∴则⊙C与AB的位置关系是相交;
故答案为:相交;
当∠A=45°时,

过C作CD⊥AB,交AB于点D.
在Rt△ACD中,∵AB=4,∠A=45°,
∴AB=AC,
∴CD=
 AB=2,
AB=2,又∵圆C的半径为2,则CD=R,
∴则⊙C与AB的位置关系是相切.
故答案为:相切.
点评:此题考查了直线与圆的位置关系,以及直角三角形的性质,直线与圆的位置关系有三种,分别为相切,相交,相离,可以利用d与r比较大小来决定,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当0≤d<r时,直线与圆相交.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 已知:如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB上的一点,且CD=AC=3,AB=4,求cosB,sin∠ADC及
已知:如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB上的一点,且CD=AC=3,AB=4,求cosB,sin∠ADC及 如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=20,AC=10,则图中等于30°的角的个数为( )
如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=20,AC=10,则图中等于30°的角的个数为( ) 如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有
如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有 如图,在Rt△ABC中,∠ACB=90°,⊙O为△ABC的外接圆,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.若⊙P与⊙O相切,则t的值是( )
如图,在Rt△ABC中,∠ACB=90°,⊙O为△ABC的外接圆,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.若⊙P与⊙O相切,则t的值是( ) 如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.