题目内容
(2013•苍梧县二模)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A,B两点,交y轴于点D,其中点B的坐标为(3,0)
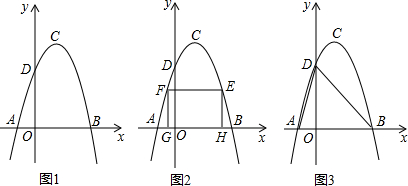
(1)求抛物线的解析式;
(2)如图2,设E是抛物线上在第一象限内的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
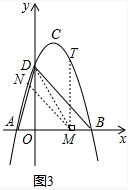
(3)如图3,在抛物线上是否存在一点T,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD?若存在,求出点T的坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)如图2,设E是抛物线上在第一象限内的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)如图3,在抛物线上是否存在一点T,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD?若存在,求出点T的坐标;若不存在,请说明理由.
分析:(1)设抛物线的解析式为:y=a(x-1)2+4,然后将点B的坐标代入函数解析式即可求得此抛物线的解析式;
(2)设E点坐标为(n,-n2+2n+3),抛物线对称轴为x=1,根据2|n-1|=EF,列方程求解;
(3)首先设M的坐标为(a,0),求得BD与DM的长,由平行线分线段成比例定理,求得MN的长,然后由相似三角形对应边成比例,即可得DM2=BD•MN,则可得到关于a的一元二次方程,解方程即可求得答案.
(2)设E点坐标为(n,-n2+2n+3),抛物线对称轴为x=1,根据2|n-1|=EF,列方程求解;
(3)首先设M的坐标为(a,0),求得BD与DM的长,由平行线分线段成比例定理,求得MN的长,然后由相似三角形对应边成比例,即可得DM2=BD•MN,则可得到关于a的一元二次方程,解方程即可求得答案.
解答:解:(1)设抛物线的解析式为:y=a(x-1)2+4,
∵点B的坐标为(3,0).
∴4a+4=0,
∴a=-1,
∴此抛物线的解析式为:y=-(x-1)2+4=-x2+2x+3;
(2)设E点坐标为(n,-n2+2n+3),抛物线对称轴为x=1,
由2(n-1)=EF,得2(n-1)=-(-n2+2n+3)或2(n-1)=-n2+2n+3,
解得n=2±
或n=±
∵n>0,
∴n=2+
或n=
,
边长EF=2(n-1)=2+2
或2
-2;
(3)存在.
过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,
∵BD=
=3
,设M(c,0),
∵MN∥BD,
∴
=
,
 即
即
=
,
∴MN=
(1+c),DM=
,
要使△DNM∽△BMD,
需
=
,即DM2=BD•MN,
可得:9+c2=3
×
(1+c),
解得:c=
或c=3(舍去).
当x=
时,y=-(
-1)2+4=
.
故存在,点T的坐标为(
,
).
∵点B的坐标为(3,0).
∴4a+4=0,
∴a=-1,
∴此抛物线的解析式为:y=-(x-1)2+4=-x2+2x+3;
(2)设E点坐标为(n,-n2+2n+3),抛物线对称轴为x=1,
由2(n-1)=EF,得2(n-1)=-(-n2+2n+3)或2(n-1)=-n2+2n+3,
解得n=2±
| 5 |
| 5 |
∵n>0,
∴n=2+
| 10 |
| 5 |
边长EF=2(n-1)=2+2
| 10 |
| 5 |
(3)存在.
过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,
∵BD=
| 32+32 |
| 2 |
∵MN∥BD,
∴
| MN |
| BD |
| AM |
| AB |
 即
即| MN | ||
3
|
| 1+c |
| 4 |
∴MN=
3
| ||
| 4 |
| 32+c2 |
要使△DNM∽△BMD,
需
| DM |
| BD |
| MN |
| DM |
可得:9+c2=3
| 2 |
3
| ||
| 4 |
解得:c=
| 3 |
| 2 |
当x=
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
故存在,点T的坐标为(
| 3 |
| 2 |
| 15 |
| 4 |
点评:此题考查了待定系数法求函数的解析式,相似三角形的判定与性质,以及平行线分线段成比例定理等知识.解题的关键是准确地用点的坐标表示线段的长,根据图形的特点,列方程求解,注意数形结合思想的应用.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
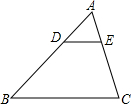 (2013•苍梧县二模)如图,△ABC中,DE∥BC,DE分别交边AB、AC于D、E两点,若AD:AB=1:3,则△ADE与四边形DBCE的面积比为
(2013•苍梧县二模)如图,△ABC中,DE∥BC,DE分别交边AB、AC于D、E两点,若AD:AB=1:3,则△ADE与四边形DBCE的面积比为 (2013•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.
(2013•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.