��Ŀ����
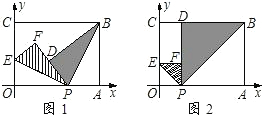
��ͼ��������y=
x2-
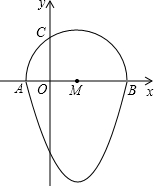
x+c�ֱ�x��ĸ�������������ڵ�A��x1��0����B��x2��0������y��ĸ����ڵ�C����tan��OAC=2tan��OBC������P�ӵ�A�������յ�B�˶���ͬʱ����Q�ӵ�B�������յ�C�˶���P��Q���˶��ٶȾ�Ϊÿ��1����λ���ȣ��ҵ�������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������˶���ʱ����t�룮

��1����˵��OB=2OA��
��2���������ߵĽ���ʽ��
��3����tΪ��ֵʱ����PBQ��ֱ�������Σ�
��4����tΪ��ֵʱ����PBQ�ǵ��������Σ�
| 3 |
| 8 |
| 3 |
| 4 |

��1����˵��OB=2OA��
��2���������ߵĽ���ʽ��
��3����tΪ��ֵʱ����PBQ��ֱ�������Σ�
��4����tΪ��ֵʱ����PBQ�ǵ��������Σ�
��1���������ã�
=2��
��OB=2OA��
��2����������ڣ�1����Ľ��۵ã�-2x1=x2��
���������߶Գ���ɵã�x1+x2=2��
x1x2=
c��
��ã�x1=-2��x2=4��c=-3��
�����ߵĽ���ʽ��y=
x2-
x-3��
��3���������ã�BP=6-t��BQ=t��
��y=
x2-
x-3��y=0���õ�3x2-6x-24=0��
��ã�x=-2��4��
��OB=4��OA=2��
�֡�OC=3��
��ֱ��������BOC�У����ݹ��ɶ����ã�BC=5��
��cos��ABC=
=
��
��ֱ��������PBQ�У���BQΪб��PBΪб�ߣ�
�ɵ�
=
��
=
��
��t=
���t=
�룻
��4����QE��AB��
��BP=6-t��BQ=t��PQ=
=
��
t=6-t��
��t=3��
��
=
��t=
�룻
��
)2=6-t��
��t=0����ȥ����t=
��
| OC |
| OA |
| OC |
| OB |
��OB=2OA��
��2����������ڣ�1����Ľ��۵ã�-2x1=x2��
���������߶Գ���ɵã�x1+x2=2��
x1x2=
| 8 |
| 3 |
��ã�x1=-2��x2=4��c=-3��
�����ߵĽ���ʽ��y=
| 3 |
| 8 |
| 3 |
| 4 |
��3���������ã�BP=6-t��BQ=t��
��y=
| 3 |
| 8 |
| 3 |
| 4 |
��ã�x=-2��4��
��OB=4��OA=2��
�֡�OC=3��
��ֱ��������BOC�У����ݹ��ɶ����ã�BC=5��
��cos��ABC=
| BO |
| BC |
| 4 |
| 5 |
��ֱ��������PBQ�У���BQΪб��PBΪб�ߣ�
�ɵ�
| 6-t |
| t |
| 4 |
| 5 |
| t |
| 6-t |
| 4 |
| 5 |
��t=
| 10 |
| 3 |
| 8 |
| 3 |
��4����QE��AB��
��BP=6-t��BQ=t��PQ=
| EQ2+PE2 |
(
|

t=6-t��
��t=3��
��
| 4t |
| 5 |
| 6-t |
| 2 |
��t=
| 30 |
| 13 |
��
(
|
��t=0����ȥ����t=
| 48 |
| 13 |

��ϰ��ϵ�д�
 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
�����Ŀ
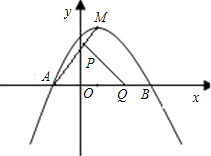 ���˶�����P��Qͬʱ�����������е�һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt���ӣ�
���˶�����P��Qͬʱ�����������е�һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt���ӣ�