题目内容
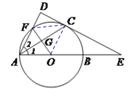
【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且![]() 于D,与⊙O交于点F.
于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线![]() 的长.
的长.

【答案】(1) AC是∠DAE的平分线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据切线的性质可得OC⊥DE,又AD⊥DE,得出AD∥OC,根据圆的半径相等得出∠1=∠OCA,再由平行线的性质得出∠2=∠OCA,等量代换即可得出结论;
(2)先证明△AOF是等边三角形,进而得出∠DAO=60°,由(1)中结论可得∠1=30°,根据直角三角形的两锐角互余可得∠E=30°,所以∠1=∠E,根据等角对等边得出CE=AC,即可得到答案.
试题解析:
解:(1)AC是∠DAE的平分线.
证明:连接![]() .
.
∵DE是⊙O的切线,∴OC⊥DE,.
∵AD⊥DE,∴∠ADC=∠OCE=![]() ,
,
∴AD∥OC,.
∴∠2=∠ACO,∵OA=OC,∴∠1=∠ACO,
∴∠1=∠2,∴AC是∠DAE的平分线.
(2)∵![]() =1 , ∴
=1 , ∴![]() ,即
,即![]() .
.
又∠1=∠2, ![]()
![]() , ∴
, ∴![]()
又![]() ,
, ![]() ∴△
∴△![]() 是等边三角形,
是等边三角形,
![]() ,
, ![]() ,.
,.
又∠ADE=![]() ,
,
∴![]() .
.
∴CE=AC=AG+CG=2.

练习册系列答案
相关题目