题目内容
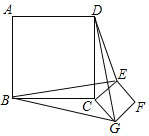
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
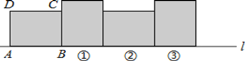
A.288πB.294πC.300πD.396π
【答案】C
【解析】
首先求得前四次旋转的路线长,发现每4次为一个循环,然后根据规律计算即可.
解:在矩形ABCD中,AB=8,BC=6,
∴AC=BD=10,
旋转第一次A的路线长是:![]() ,
,
旋转第二次A的路线长是:![]() ,
,
旋转第三次A的路线长是:![]() ,
,
旋转第四次A的路线长是:0,
以此类推,每四次为一个循环,
故顶点A旋转四次经过的路线长为:4π+5π+3π=12π,
∵99÷4=24…3,
∴顶点A旋转99次经过的路线长为:12π×25=300π,
故选:C.

练习册系列答案
相关题目
【题目】基础知识考查:
(1)一次函数表达式 ,当k>0,b>0时,图像经过 象限;当k>0,b<0时,图像经过 象限;当k<0,b>0时,图像经过 象限;当k<0,b<0时,图像经过 象限.特别当b=0时,图像经过 ,称为 函数.
(2)反比例函数三种表达方式分别为: 、 、 反比例函数的图像称为 ,当k>0时,图像在 和 象限,y随x的增大而 ;当k<0时,图像在 和 象限,y随x的增大而 .
(3)特殊三角函数值:
0° | 30° | 45° | 60° | 90° | |
sinA | |||||
cosA | |||||
tanA | |||||
cotA |
(4)二次函数表达式:
①一般式: ;
②顶点式: ; ; ;
.
③交点式(点式): ;
④对称轴公式: 顶点坐标公式: .
⑤二次函数图像称为 ,当a>0时,图像开口向 ;当a<0时,图像开口向 .c>0时,图像和 轴正半轴相交,c<0时,图像和 轴负半轴相交.