题目内容
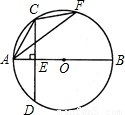
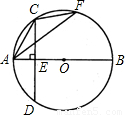
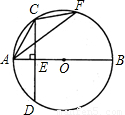
 如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为
如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为
- A.

- B.

- C.

- D.以上都不对
A
分析:连接BC,利用垂径定理求得EC的长,然后在直角△BCE中利用勾股定理求得BC的长,依据圆周角定理∠AFC=∠CBE,则在直角△BCE中,求∠CBE的正弦值即可.
解答: 解:连接BC.
解:连接BC.
∵弦CD⊥AB于E,
∴CE= CD=
CD= ×8=4.
×8=4.
∴在直角△BCE中,BC= =
=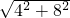 =4
=4 ,
,
则sin∠AFC=sin∠CBE= =
=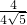 =
= .
.
故选A.
点评:本题考查了圆周角定理、垂径定理、勾股定理以及三角函数,正确理解定理是关键.
分析:连接BC,利用垂径定理求得EC的长,然后在直角△BCE中利用勾股定理求得BC的长,依据圆周角定理∠AFC=∠CBE,则在直角△BCE中,求∠CBE的正弦值即可.
解答:
 解:连接BC.
解:连接BC.∵弦CD⊥AB于E,
∴CE=
 CD=
CD= ×8=4.
×8=4.∴在直角△BCE中,BC=
 =
=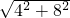 =4
=4 ,
,则sin∠AFC=sin∠CBE=
 =
=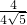 =
= .
.故选A.
点评:本题考查了圆周角定理、垂径定理、勾股定理以及三角函数,正确理解定理是关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
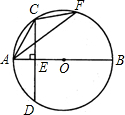 如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.
如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.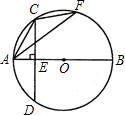 如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.
如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.