Question

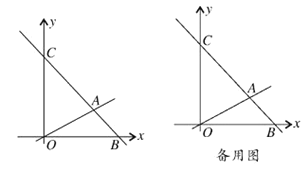
【题目】如图，在平面直角坐标系中，直线与轴和轴分别交于点和点，与直线相交于点，，动点在线段和射线上运动．

（1）求点和点的坐标．

（2）求的面积．

（3）是否存在点，使的面积是的面积的？若存在，求出此时点的坐标，若不存在，说明理由．

Answer 1

【答案】（1），；（2）12；（3）的坐标是或或

【解析】

（1）分别令x=0，y=0进行求解即可得到B，C的坐标；

（2）利用三角形的面积公式进行计算即可得解；

（3）对M进行分类，当M在线段OA上和当M在射线AC上运动两种情况进行讨论即可得解.

（1）直线，令x=0，得y=6，即，令y=0，得x=6，则；

（2）∵,，

∴OC=6，

∴；

（3）存在点，使的面积是的面积的，

设，OA的解析式为，则，

解得，则OA的解析式为，

∵当时，即，

又∵，

∴，

当M在线段OA上时，，

∴时，，则点的坐标是；

当M在射线AC上时，即在射线上时，

∴时，，则点的坐标是；时，，则点的坐标是，

综上所述，的坐标是或或.