题目内容
如图，坐标平面上二次函数y=x2+1的图形通过A、B两点，且坐标分别为（a，
）、（b，），则AB的长度为何？
- A.5
- B.
- C.
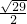
- D.
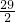
A
分析：将纵坐标的值代入函数式求横坐标a、b的值，根据AB=|a-b|求解．
解答：把y=代入y=x2+1中，得=x2+1，
即x2=，解得x=±
，
∴a=，b=-，
∴AB=-（-）=5．
故选A．
点评：本题考查了二次函数图象上点的坐标特点．关键是明确抛物线上纵坐标相等的两点关于对称轴对称．
分析：将纵坐标的值代入函数式求横坐标a、b的值，根据AB=|a-b|求解．
解答：把y=
代入y=x2+1中，得=x2+1，即x2=
，解得x=±，∴a=
，b=-，∴AB=
-（-）=5．故选A．
点评：本题考查了二次函数图象上点的坐标特点．关键是明确抛物线上纵坐标相等的两点关于对称轴对称．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，坐标平面上二次函数y=x2+1的图形通过A、B两点，且坐标分别为（a，| 29 |
| 4 |
| 29 |
| 4 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
如图为坐标平面上二次函数y=ax2+bx+c的图形，且此图形通（-1，1）、（2，-1）两点．下列关于此二次函数的叙述，何者正确（ ）| A、y的最大值小于0 | B、当x=0时，y的值大于1 | C、当x=1时，y的值大于1 | D、当x=3时，y的值小于0 |
的图形，且此图形通（－1 , 1）、（2 ,－1）两点．下列关于此二次函数的叙述，何者正确？(
)
