Question

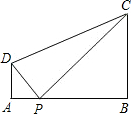如图，∠A=∠B=90°，AB=7，AD=2，BC=3，如果边AB上的点P使得以P，A，D为顶点的三角形和以P，B，C为顶点的三角形相似，则这样的P点共有几个（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

分析：根据相似三角形的判定与性质，当若点A，P，D分别与点B，C，P对应，与若点A，P，D分别与点B，P，C对应，分别分析得出AP的长度即可．

解答：解：若点A，P，D分别与点B，C，P对应，即△APD∽△BCP，
∴

AD

BP

=

AP

BC

，
∴

2

7-AP

=

AP

3

，
∴AP²-7AP+6=0，
∴AP=1或AP=6，
检测：当AP=1时，由BC=3，AD=2，BP=6，
∴

AP

BC

=

AD

BP

，
又∵∠A=∠B=90°，
∴△APD∽△BCP．
当AP=6时，由BC=3，AD=2，BP=1，
又∵∠A=∠B=90°，
∴△APD∽△BCP．
若点A，P，D分别与点B，P，C对应，即△APD∽△BPC．
∴

AP

BP

=

AD

BC

，
∴

AP

7-AP

=

2

3

，
∴AP=

14

5

．
检验：当AP=

14

5

时，∵BP=

21

5

，AD=2，BC=3，
∴

AP

BP

=

AD

BC

，
又∵∠A=∠B=90°，
∴△APD∽△BPC．
因此，点P的位置有三处，即在线段AP的长为1、

14

5

、6，
故选C．

点评：本此题考查了相似三角形的判定和性质，根据P点不同位置进行分析，解题时要注意一题多解的情况，要注意别漏解是解题关键