题目内容
梯形ABCD中,AD∥BC,AB=4cm,AD=6cm,BC=12cm,∠B=30°,现点P从B点出发,沿BA→AD向点D运动,点Q从点C出发,沿CB向点B运动,P、Q的运动速度均为1cm/s,两点中有一点到达目的地时,另一点也停止运动,
(1)请用含有t的代数式表示S△PBQ;
(2)在整个运动过程中,是否存在某一时刻,A、B、Q、P四点恰好构成一个平行四边形?若存在,请求出t的值;若不存在,请说明理由.

考点:
平行四边形的性质;梯形..
专题:
动点型.
分析:
(1)有两种情况,即P在AB上时和P在AD上时,在这两种情况中,BQ的长都能表示为(12﹣t),关键是P到BC的距离,当P在AB上时,PB=t,由于∠B=30°,所以此时高为0.5t,当P在AD上时,P到BC的距离和A到BC的距离相等为2,所以面积就可求出了.
(2)要成为平行四边形则必须AP=BQ,即t﹣4=12﹣t,解方程即可解答.
解答:
解:(1)①当P在AB上时,过P作PH⊥BC于H,t秒后,BP=tcm,
∵∠B=30°,
∴PH=![]() t,BQ=12﹣t,
t,BQ=12﹣t,
∴S△PBQ=![]() t(12﹣t)(0≤t≤4)
t(12﹣t)(0≤t≤4)
②当P在AD上时,过P作PH⊥BC于H,PH=![]() AB=2
AB=2
S△PBQ=(12﹣t)×2×![]() =12﹣t(4<t≤10)
=12﹣t(4<t≤10)
(2)能;当P点运动t秒后,在线段AD上时,A、B、Q、P能构成一个平行四边形,
此时,AP∥BQ且AP=BQ,可得t﹣4=12﹣t,解得,t=8,
所以,运动8s后,A、B、Q、P四点恰好构成一个平行四边形.

点评:
此题主要考查了平行四边形的判定,以及变量之间的函数关系,难易程度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
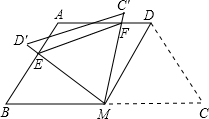 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点. DE.
DE. 如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.
如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.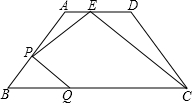 如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是
如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是 分别交边CD、BC于点F、E,若AD=3,BC=12,
分别交边CD、BC于点F、E,若AD=3,BC=12,