��Ŀ����
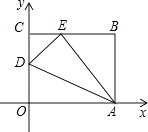
����Ŀ����ͼ1��������![]() ��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��1����m��n��ֵ��
��2����ͼ2����NΪ�������ϵ�һ���㣬��λ��ֱ��BC�Ϸ�������CN��BN������NBC��������ֵ��
��3����ͼ3����M��P�ֱ�Ϊ�߶�BC���߶�OB�ϵĶ��㣬����PM��PC���Ƿ���������ĵ�P��ʹ��PCMΪ���������Σ���PMBΪֱ��������ͬʱ�����������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��m=1��n=��9����2��![]() ����3��P��
����3��P��![]() ��0����
��0����![]() ��0����
��0����
��������
�����������1���������ߵĽ���ʽΪ![]() =
=![]() ���������ߵĶԳ���Ϊֱ��x=2������A�͵�BΪ�ԳƵ㣬��2����m��2��=2m+3��2�����m=1����A����1��0����B��5��0������A����1��0������
���������ߵĶԳ���Ϊֱ��x=2������A�͵�BΪ�ԳƵ㣬��2����m��2��=2m+3��2�����m=1����A����1��0����B��5��0������A����1��0������![]() ��9+n=0�����n=��9��
��9+n=0�����n=��9��
��2����ND��y�ύBC��D����ͼ2�������߽���ʽΪ![]() =
=![]() ����x=0ʱ��y=3����C��0��3������ֱ��BC�Ľ���ʽΪy=kx+b����B��5��0����C��0��3�������
����x=0ʱ��y=3����C��0��3������ֱ��BC�Ľ���ʽΪy=kx+b����B��5��0����C��0��3�������![]() �������
�������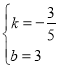 ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ![]() ����N��x��
����N��x��![]() ������D��x��
������D��x��![]() ������ND=
������ND=![]() =
=![]() ����S��NBC=S��NDC+S��NDB=
����S��NBC=S��NDC+S��NDB=![]() 5ND=
5ND=![]() =
=![]() ����x=
����x=![]() ʱ����NBC���������ֵΪ
ʱ����NBC���������ֵΪ![]() ��
��
��3�����ڣ�
��B��5��0����C��0��3������BC=![]() =
=![]() ��������������ۣ�
��������������ۣ�
������PMB=90�㣬����PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=![]() ��t���ߡ�MBP=��OBC�����BMP�ס�BOC����
��t���ߡ�MBP=��OBC�����BMP�ס�BOC����![]() ����
����![]() �����t=
�����t=![]() ��BP=
��BP=![]() ����OP=OB��BP=5��
����OP=OB��BP=5��![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��0����
��0����
������MPB=90�㣬��MP=MC����PM=t����CM=t��MB=![]() ��t���ߡ�MBP=��CBO�����BMP�ס�BCO����
��t���ߡ�MBP=��CBO�����BMP�ס�BCO����![]() ����
����![]() �����t=
�����t=![]() ��BP=
��BP=![]() ����OP=OB��BP=5��
����OP=OB��BP=5��![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��0����
��0����
����������P��������![]() ��0����
��0����![]() ��0����
��0����

����Ŀ��ij��ѧ���������15��ѧ�����˽�����һ����У����������ʱ�䣬������±���ʾ��
һ����У����������ʱ�䣨Сʱ�� | 5 | 6 | 7 | 8 |
���� | 2 | 5 | 6 | 2 |
��ô��15��ѧ����һ����У�μ�����������ʱ�����λ���� Сʱ��