题目内容
 如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为________.
如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为________.
26
分析:根据全等三角形对应角相等,可以证明AC∥DE∥HF,再根据全等三角形对应边相等BC=CE=EF,然后利用平行线分线段成比例定理求出AB=3KE,PC=2KE,得出△DMP≌△EMK,S△MEK=2,M是DE的中点,再由相似三角形的性质即可得出答案.
解答:∵△ABC≌△DCE≌△HEF,
∴∠ACB=∠DEC=∠HFE,BC=CE=EF,
∴AC∥DE∥HF,
 =
=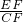 =
= ,
, =
= =
= ,
,
∴AB=3KE,PC=2KE,
∴PD=KE,
∵∠D=∠MEK,∠DMP=∠EMK,
∴△DMP≌△EMK,
∴S△MEK=2,M是DE的中点,
∴S△EFK=2S△EMK=4,
∵△EFK∽△CFP,相似比为1:2,
∴S四边形PCEM=S△PCF-S△EFK-S△MEK=16-4-2=10,
∴S△ABC=10+2=12,
∴三个阴影部分面积=S△ABC+S四边形PCBM+S△EFK=12+10+4=26.
故答案为26.
点评:本题主要利用全等三角形的性质,找出阴影部分的图形边的关系和三角形的面积公式的解题的关键.
分析:根据全等三角形对应角相等,可以证明AC∥DE∥HF,再根据全等三角形对应边相等BC=CE=EF,然后利用平行线分线段成比例定理求出AB=3KE,PC=2KE,得出△DMP≌△EMK,S△MEK=2,M是DE的中点,再由相似三角形的性质即可得出答案.
解答:∵△ABC≌△DCE≌△HEF,
∴∠ACB=∠DEC=∠HFE,BC=CE=EF,
∴AC∥DE∥HF,

 =
=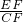 =
= ,
, =
= =
= ,
,∴AB=3KE,PC=2KE,
∴PD=KE,
∵∠D=∠MEK,∠DMP=∠EMK,
∴△DMP≌△EMK,
∴S△MEK=2,M是DE的中点,
∴S△EFK=2S△EMK=4,
∵△EFK∽△CFP,相似比为1:2,
∴S四边形PCEM=S△PCF-S△EFK-S△MEK=16-4-2=10,
∴S△ABC=10+2=12,
∴三个阴影部分面积=S△ABC+S四边形PCBM+S△EFK=12+10+4=26.
故答案为26.
点评:本题主要利用全等三角形的性质,找出阴影部分的图形边的关系和三角形的面积公式的解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
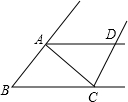 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
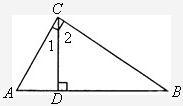
 ,且CB=CE.
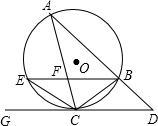
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.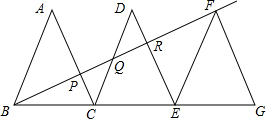 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且