题目内容
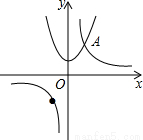
 已知函数y=x2与y=-x+1图象交点的横坐标就是一元二次方程y=x2+x-1的解,如图,抛物线y=x2+1与双曲线y=
已知函数y=x2与y=-x+1图象交点的横坐标就是一元二次方程y=x2+x-1的解,如图,抛物线y=x2+1与双曲线y=| k |
| x |
| k |
| x |
-1<x<0
-1<x<0
.分析:把A点的横坐标1代入抛物线y=x2+1,求出点A的坐标,代入y=
中求的值,再求式
<-x2-1的解集,确定不等式
+x2+1<0的解.
| k |
| x |
| 2 |
| x |
| k |
| x |
解答: 解:当x=1时,y=x2+1=2,
解:当x=1时,y=x2+1=2,
∴A(1,2);
k=xy=1×2=2,即y=
,
解方程
+x2+1=0,
实际就是求出y=
,与y=-x2-1,交点进而得出
<-x2-1的解集,
∵y=
,与y=-x2-1,交点横坐标为:x=-1,
由图象可知,不等式
<-x2-1的解集就是
+x2+1<0的解集,
得出:-1<x<0.
故答案为:-1<x<0.
 解:当x=1时,y=x2+1=2,
解:当x=1时,y=x2+1=2,∴A(1,2);
k=xy=1×2=2,即y=
| 2 |
| x |
解方程
| 2 |
| x |
实际就是求出y=
| 2 |
| x |
| 2 |
| x |
∵y=
| 2 |
| x |
由图象可知,不等式
| 2 |
| x |
| k |
| x |
得出:-1<x<0.
故答案为:-1<x<0.
点评:本题主要考查了二次函数与不等式的关系.关键是根据题意求反比例函数解析式,求出二次函数与反比例函数解析式和为0时x的值.

练习册系列答案
相关题目
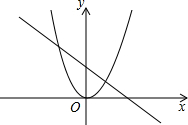 已知函数y1=x2与函数y2=-
已知函数y1=x2与函数y2=-| 1 |
| 2 |
A、-
| ||
B、x>2或x<-
| ||
C、-2<x<
| ||
D、x<-2或x>
|
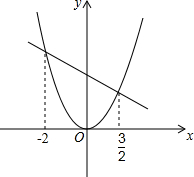 (2011•赣州模拟)已知函数y1=x2与y2=-
(2011•赣州模拟)已知函数y1=x2与y2=-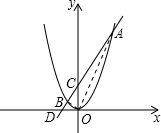 已知函数y=x2与y=2x+3的交点为A,B(A在B的右边).
已知函数y=x2与y=2x+3的交点为A,B(A在B的右边).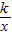 的交点A的横坐标是1,则关于x的不等式
的交点A的横坐标是1,则关于x的不等式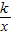 +x2+1<0的解集是 .
+x2+1<0的解集是 .