Question

【题目】如图，已知直线y=﹣2x+8与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．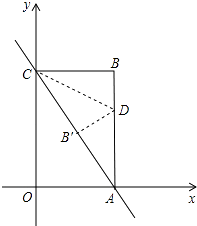

（1）求点A、C的坐标；
（2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式；
（3）在（2）的条件下，坐标平面内是否存在点P（除点B外），使得△APC与△ABC全等？若存在，直接写出符合条件的点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：令y=0，则﹣2x+8=0，解得x=4，
∴A（4，0），
令x=0，则y=8，
∴C（0，8）
（2）解：由折叠可知：CD=AD，
设AD=x，则CD=x，BD=8﹣x，
由题意得，（8﹣x）2+42=x2 ，
解得x=5，
此时AD=5，
∴D（4，5），
设直线CD为y=kx+8，
把D（4，5）代入得5=4k+8，解得k=﹣ ，
∴直线CD的解析式为y=﹣ x+8
（3）解：①当点P与点O重合时，△APC≌△CBA，此时P（0，0）
②当点P在第一象限时，如图1，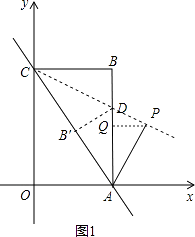

由△APC≌△CBA得∠ACP=∠CAB，
则点P在直线CD上．过P作PQ⊥AD于点Q，
在Rt△ADP中，
AD=5，AP=BC=4，PD=BD=8﹣5=3，
由AD×PQ=DP×AP得：5PQ=3×4，
∴PQ= ，
∴xP=4+ = ，把x= 代入y=﹣ x+8得y= ，
此时P（ ， ）
③当点P在第二象限时，如图2，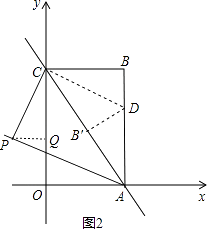

同理可求得：PQ= ，
在RT△PCQ中，CQ= = = ，
∴OQ=8﹣ = ，
此时P（﹣ ， ），
综上，满足条件的点P有三个，分别为：（0，0），（ ， ），（﹣ ， ）
【解析】（1）已知直线y=-2x+8与x轴、y轴分别交于点A、C，即可求得A和C的坐标。
（2）根据题意可知△ACD是等腰三角形，求出AD长即可求得D点坐标，最后即可求出CD的解析式。
（3）将点P在不同象限进行分类，根据全等三角形的判定方法找出所有全等三角形，找出符合题意的点P的坐标。