Question

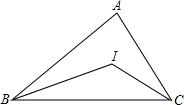如图，已知BI、CI分别是∠ABC、∠ACB的角平分线，且∠A=70°，则∠BIC=

 

度．

Answer 1

考点：三角形内角和定理

专题：

分析：根据三角形的内角和定理和角平分线的定义求出∠IBC+∠ICB，再根据三角形的内角和定理列式计算即可得解．

解答：解：∵BI、CI分别是∠ABC、∠ACB的角平分线，
∴∠IBC+∠ICB=

1

2

∠ABC+

1

2

∠ACB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A），
∵∠A=70°，
∴∠IBC+∠ICB=

1

2

（180°-70°）=55°，
∴∠BIC=180°-（∠IBC+∠ICB）=180°-55°=125°．
故答案为：125．

点评：本题考查了三角形的内角和定理，角平分线的定义，整体思想的利用是解题的关键．