题目内容
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y= ![]() x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
【答案】
(1)
解:∵x是整数,x≠0时, ![]() x是一个无理数,
x是一个无理数,
∴x≠0时, ![]() x+2不是整数,
x+2不是整数,
∴x=0,y=2,
即函数y= ![]() x+2的图象上“中国结”的坐标是(0,2)
x+2的图象上“中国结”的坐标是(0,2)
(2)
解:①当k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:
(k≠0,k为常数)的图象上有且只有两个“中国结”:
(1,1)、(﹣1、﹣1);
②当k=﹣1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:
(k≠0,k为常数)的图象上有且只有两个“中国结”:
(1,﹣1)、(﹣1,1).
③当k≠±1时,函数y= ![]() (k≠0,k为常数)的图象上最少有4个“中国结”:
(k≠0,k为常数)的图象上最少有4个“中国结”:
(1,k)、(﹣1,﹣k)、(k,1)、(﹣k,﹣1),这与函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”矛盾,
(k≠0,k为常数)的图象上有且只有两个“中国结”矛盾,
综上可得,k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);
k=﹣1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,﹣1)、(﹣1、1).
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,﹣1)、(﹣1、1).
(3)
解:令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,
则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,
∴ 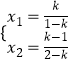
∴k= ![]() ,
,
整理,可得
x1x2+2x2+1=0,
∴x2(x1+2)=﹣1,
∵x1、x2都是整数,
∴ ![]() 或
或 ![]()
∴ ![]() 或
或 ![]()
①当 ![]() 时,
时,
∵ ![]() ,
,
∴k= ![]() ;
;
②当 ![]() 时,
时,
∵ ![]() ,
,
∴k=k﹣1,无解;
综上,可得
k= ![]() ,x1=﹣3,x2=1,
,x1=﹣3,x2=1,
y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k
=[ ![]() 2﹣3×
2﹣3× ![]() +2]x2+[2×(
+2]x2+[2×( ![]() )2﹣4×
)2﹣4× ![]() +1]x+(
+1]x+( ![]() )2﹣
)2﹣ ![]()
=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
①当x=﹣2时,
y=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
= ![]() ×(﹣2)2
×(﹣2)2 ![]() ×(﹣2)+
×(﹣2)+ ![]()
= ![]()
②当x=﹣1时,
y=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
= ![]() ×(﹣1)2
×(﹣1)2 ![]() ×(﹣1)+
×(﹣1)+ ![]()
=1
③当x=0时,y= ![]() ,
,
另外,该函数的图象与x轴所围成的平面图形中x轴上的“中国结”有3个:
(﹣2,0)、(﹣1、0)、(0,0).
综上,可得
若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,
该函数的图象与x轴所围成的平面图形中(含边界),一共包含有6个“中国结”:(﹣3,0)、(﹣2,0)、(﹣1,0)(﹣1,1)、(0,0)、(1,0)
【解析】(1)因为x是整数,x≠0时, ![]() x是一个无理数,所以x≠0时,
x是一个无理数,所以x≠0时, ![]() x+2不是整数,所以x=0,y=2,据此求出函数y=
x+2不是整数,所以x=0,y=2,据此求出函数y= ![]() x+2的图象上所有“中国结”的坐标即可.(2)首先判断出当k=1时,函数y=
x+2的图象上所有“中国结”的坐标即可.(2)首先判断出当k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);然后判断出当k≠1时,函数y=
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);然后判断出当k≠1时,函数y= ![]() (k≠0,k为常数)的图象上最少有4个“中国结”,据此求出常数k的值与相应“中国结”的坐标即可.(3)首先令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,求出x1、x2的值是多少;然后根据x1、x2的值是整数,求出k的值是多少;最后根据横坐标,纵坐标均为整数的点称之为“中国结”,判断出该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”即可.
(k≠0,k为常数)的图象上最少有4个“中国结”,据此求出常数k的值与相应“中国结”的坐标即可.(3)首先令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,求出x1、x2的值是多少;然后根据x1、x2的值是整数,求出k的值是多少;最后根据横坐标,纵坐标均为整数的点称之为“中国结”,判断出该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”即可.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案