题目内容
已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.
现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为 ,△AMN的面积为
,△AMN的面积为 .
.
(1)试确定△AMN存在时,路程 的取值范围.
的取值范围.
(2)请你求出面积S关于路程 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?


(1)路程 的取值范围(0,10).当
的取值范围(0,10).当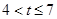 时,
时,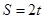 ;
;
当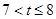 时,
时,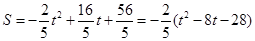 ;
;
当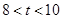 时,
时,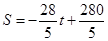 .
.
(3)当点M前进的路程为7时,△AMN的面积最大,最大为14
解析试题分析:解:(1)已知AD=CD=4,过C作CE⊥AB可得AE=CD=4,EB=3.所以在Rt△CEB中,
CE=AD=4,则CB=5.可知四边形ABCD四边的和=4+4+5+7=20.所以2t=20.则
路程 的取值范围(0,10).
的取值范围(0,10).
(2)当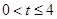 时,
时,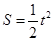 ;
;
当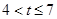 时,
时,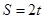 ;
;
当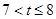 时,
时,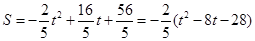 ;
;
当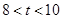 时,
时,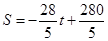 .
.
(3)由(2)可知:当点M前进的路程为7时,△AMN的面积最大,最大为14.
考点:几何与函数结合
点评:本题难度较大。学生需要运用学过的几何与函数只是相结合来解题计算。

练习册系列答案
相关题目
已知四边形ABCD中,给出下列四个论断:(1)AB∥CD,(2)AB=CD,(3)AD=BC,(4)AD∥BC.以其中两个论断作为条件,余下两个作为结论,可以构成一些命题.在这些命题中,正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、6个 |
选做题:(A)已知四边形ABCD中,AD∥BC,对角线AC、BD交于点O,∠OBC=∠OCB,并且 ,求证:四边形ABCD是 形.(要求在已知条件中的横线上补上一个条件 ,在求证中的横线上添上该四边形的形状,然后画出图形,予以证明,证明时要用上所有条件)
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
按这种增长趋势,请你算一算2006年该市的财政收入是多少亿元.
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
 如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD= 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,