题目内容
 如图△ABC中边BC所在直线与圆相切于C点,边AC交圆于另一点D,若∠A=70°,∠B=60°,则劣弧
如图△ABC中边BC所在直线与圆相切于C点,边AC交圆于另一点D,若∠A=70°,∠B=60°,则劣弧 | CD |
100°
100°
.分析:先根据据三角形的内角和定理求出∠ACB的度数,再根据弦切角等于它所夹的弧的度数的一半进行求解.
解答:解:∵∠A=70°,∠B=60°,
∴∠ACB=50°,
又∵圆与直线BC相切于C点,
∴
的度数=2∠ACB=50°×2=100°.
故答案为100°.
∴∠ACB=50°,
又∵圆与直线BC相切于C点,
∴
 |
| CD |
故答案为100°.
点评:本题考查了切线的性质及三角形的内角和定理,熟知三角形的内角和是180°,弦切角等于它所夹的弧所对的圆周角,圆周角等于它所对的弧所对的圆心角的一半等知识是解答此题的关键.

练习册系列答案
相关题目
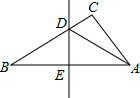 如图△ABC中边AB的垂直平分线分别交BC,AB于点D、E,AE=3cm,△ADC的周长为9cm,求△ABC的周长.
如图△ABC中边AB的垂直平分线分别交BC,AB于点D、E,AE=3cm,△ADC的周长为9cm,求△ABC的周长. 如图△ABC中边BC所在直线与圆相切于C点,边AC交圆于另一点D,若∠A=70°,∠B=60°,则劣弧
如图△ABC中边BC所在直线与圆相切于C点,边AC交圆于另一点D,若∠A=70°,∠B=60°,则劣弧 的度数是________.
的度数是________. 如图△ABC中边AB的垂直平分线分别交BC,AB于点D、E,AE=3cm,△ADC的周长为9cm,求△ABC的周长.
如图△ABC中边AB的垂直平分线分别交BC,AB于点D、E,AE=3cm,△ADC的周长为9cm,求△ABC的周长.