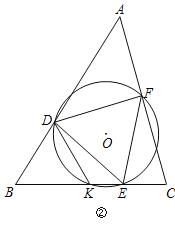题目内容
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?

【答案】(1) 2或![]() ;(2) 3秒,15cm2.
;(2) 3秒,15cm2.
【解析】
(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过2或![]() s后,P、Q两点的距离为4
s后,P、Q两点的距离为4![]() cm;(2)根据三角形的面积公式S△PCQ=
cm;(2)根据三角形的面积公式S△PCQ=![]() ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
:(1)∵在Rt△ABC中,AC=8cm,BC=6cm,
∴AB=10cm,
设经过ts后,P、Q两点的距离为4![]() cm,
cm,
ts后,PC=6-t cm,CQ=2t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(6-t)2+(2t)2=(4![]() )2;
)2;
解得t=2或t=![]() ,
,
故t为2或![]() 时,P、Q两点的距离为4
时,P、Q两点的距离为4![]() cm;
cm;
(2)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=6-tcm,CQ=2t cm,
S△PCQ=![]() ×PC×CQ=
×PC×CQ=![]() ×(6-t)×2t=-t2+6t
×(6-t)×2t=-t2+6t
当t=-![]() 时,即t=3s时,△PCQ的面积最大,
时,即t=3s时,△PCQ的面积最大,
即S△PCQ=![]()
×PC×CQ=![]() ×(6-3)×6=9(cm2),
×(6-3)×6=9(cm2),
∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大=![]() ×6×8-9=15(cm2),
×6×8-9=15(cm2),
当点P运动3秒时,四边形BPQA的面积最小为:15cm2.

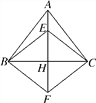
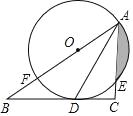
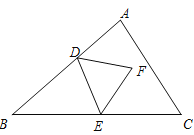
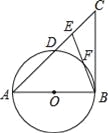
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.