Question

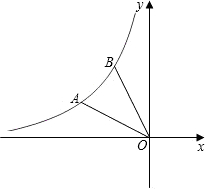已知反比例函数y=-

3

x

的图象经过点A（m，1）．
（1）求m的值．
（2）点O是坐标原点，将线段OA绕点O顺时针旋转30°得到线段OB，判断点B是否在反比例函数的图象上，并说明理由．

Answer 1

分析：（1）本题需先把点A的坐标代入反比例函数的解析式即可求出m的值．
（2）本题需先过点A作x轴的垂线，得出OA的值，再过点B作x轴的垂线，求出BD、OD的长，从而得出点B的坐标，即可得出点B在反比例函数的图象上．

解答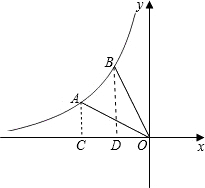：解：（1）由题意得：1=-

3

m

，
解得：m=-

3

（2）过点A作x轴的垂线交x轴于点C，
在Rt△AOC中，OC=

3

，AC=1
可得OA=

OC2+AC2

=2，
∴AC=

1

2

OA，
∴∠AOC=30°
由题意，∠AOC=30°，OB=OA=2，
∴∠BOC=60°
过点B作x轴的垂线交x轴于点D，
在Rt△BOD中，可得，BD=

3

，OD=1
∴点B坐标（-1，

3

），
将x=-1代入y=-

3

x

中，得y=

3

．
∴点B（-1，

3

）在反比例函数y=-

3

x

的图象上．

点评：本题主要考查了反比例函数的综合应用，在解题时要注意作辅助线，并与解直角三角形相结合是本题的关键．