题目内容
 如图,两个等圆圆O1,O2外切,O1A、O1B分别与圆O2切于点A、B.设∠AO1B=α,若A(sinα,0),B(cosα,0)为抛物线y=x2+bx+c与x轴的两个交点,则b=
如图,两个等圆圆O1,O2外切,O1A、O1B分别与圆O2切于点A、B.设∠AO1B=α,若A(sinα,0),B(cosα,0)为抛物线y=x2+bx+c与x轴的两个交点,则b=分析:连接O1O2,O2A,O2B,根据切线的性质得到直角三角形,再由直角三角形中边的关系得到角的度数,确定A,B两点的坐标,用待定系数法可以求出b,c的值.
解答: 解:如图:
解:如图:
连接O1O2,O2A,O2B,
∵O1A,O1B是⊙O2的切线,∴O1A⊥O2A,O1B⊥O2B,
又因为两圆是等圆,所以O1O2=2O2A,得∠AO1O2=30°
∴∠AO1B=60°,即:α=60°,
∴A(
,0)B(
,0).
把A,B两点的坐标代入抛物线得:
,
解方程组得:
.
故答案为:-
,
.
 解:如图:
解:如图:连接O1O2,O2A,O2B,
∵O1A,O1B是⊙O2的切线,∴O1A⊥O2A,O1B⊥O2B,
又因为两圆是等圆,所以O1O2=2O2A,得∠AO1O2=30°
∴∠AO1B=60°,即:α=60°,
∴A(
| ||
| 2 |
| 1 |
| 2 |
把A,B两点的坐标代入抛物线得:
|
解方程组得:
|
故答案为:-
| ||
| 2 |
| ||
| 4 |
点评:本题考查的是解直角三角形,根据直线与圆相切,连接圆心和切点,得到直角三角形,再根据两圆是等圆得到∠α的度数,确定A,B两点的坐标,代入二次函数中求出b,c的值.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
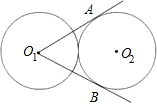 如图,两个等圆圆O1,O2外切,O1A、O1B分别与圆O2切于点A、B.设∠AO1B=α,若A(sinα,0),B(cosα,0)为抛物线y=x2+bx+c与x轴的两个交点,则b=________,c=________.
如图,两个等圆圆O1,O2外切,O1A、O1B分别与圆O2切于点A、B.设∠AO1B=α,若A(sinα,0),B(cosα,0)为抛物线y=x2+bx+c与x轴的两个交点,则b=________,c=________.