��Ŀ����
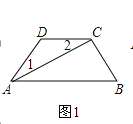
����Ŀ��(1)��ͼ��ACƽ�֡�DAB����1=��2����˵��AB��CD��λ�ù�ϵ��������֤����
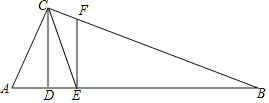
(2)��ͼ��AB��CD��AB���·�����E��F����:BFƽ�֡�ABE��DFƽ�֡�CDE������DFB=20������CDE=70�������ABE�Ķ�����
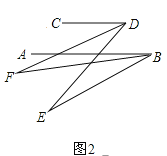
(3)��ǰ��������£���P��BE��һ�㣬G��CD����һ�㣬PQƽ�֡�BPG��PQ��GN��GMƽ�֡�DGP�����н���:�١�DGP-��MGN��ֵ���䣻�ڡ�MGN�Ķ������䣬����֤��ֻ��һ������ȷ�ģ�����������ȷ��ѡ����ֵ.

���𰸡���1��AB��CD����2����ABE=30������3���ڡ�MGN�Ķ���Ϊ15�㲻�䣬֤��������.
��������
��1�������ڴ�����ȣ���ֱ��ƽ��֤�����ɣ�
��2�����ɽ�ƽ���ߵĶ���ɵã���CDF��![]() ��CDE=35������ABE=2��ABF��Ȼ�������ֱ��ƽ���ڴ�����ȣ��ɵã���2=��CDF=35����Ȼ��������������ǵ����������ABF�Ķ��������������ABE�Ķ�����
��CDE=35������ABE=2��ABF��Ȼ�������ֱ��ƽ���ڴ�����ȣ��ɵã���2=��CDF=35����Ȼ��������������ǵ����������ABF�Ķ��������������ABE�Ķ�����
��3�����������ε�һ����ǵ������������ڵ������ڽǵĺͿɵá�1=��BPG+��B���ٸ���ƽ���ߵ������Լ���ƽ���ߵĶ����ʾ����MGP����DPQ��������ֱ��ƽ�У��ڴ�����ȿɵá�NGP=��GPQ��Ȼ����ʽ��ʾ����MGN=![]() ��B���Ӷ��ж�����ȷ��
��B���Ӷ��ж�����ȷ��
��1�����ۣ�AB��CD��
֤������ACƽ�֡�DAB��
���1=��CAB��
�ߡ�1=��2��
���2=��CAB��
��AB��CD��
��2���⣺��ͼ2��
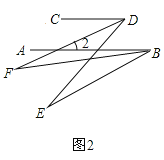
��BFƽ�֡�ABE��DFƽ�֡�CDE��
���CDF��![]() ��CDE=35������ABE=2��ABF��
��CDE=35������ABE=2��ABF��
��CD��AB��
���2=��CDF=35����
�ߡ�2=��DFB+��ABF����DFB=20����
���ABF=15����
���ABE=2��ABF=30����
��3���⣺�ڽ���MGN�Ķ���Ϊ15�����䣮
��ͼ3�����������ε�������ʣ���1=��BPG+��B��
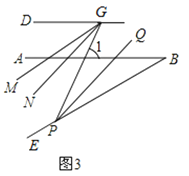
��PQƽ�֡�BPG��GMƽ�֡�DGP��
���GPQ=![]() ��BPG����MGP=
��BPG����MGP=![]() ��DGP��
��DGP��
��AB��CD��
���1=��DGP��
���MGP=![]() ����BPG+��B����
����BPG+��B����
��PQ��GN��
���NGP=��GPQ=![]() ��BPG��
��BPG��
���MGN=��MGP-��NGP=![]() ����BPG+��B��-
����BPG+��B��-![]() ��BPG=
��BPG=![]() ��B��
��B��
����ǰ�����������B=30����
���MGN=![]() ��30��=15����
��30��=15����
��١�DGP-��MGN��ֵ���DGP�ı仯���仯���ڡ�MGN�Ķ���Ϊ15�����䣮

 �������ϵ�д�
�������ϵ�д�