题目内容
 为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为________.
为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为________.
10cm
分析:首先连接OA,过点O作OE⊥AB,交⊙O于F,根据垂径定理,即可求得AE的值,然后在Rt△OAE中,利用勾股定理,即可求得OE的值,继而求得污水的最大深度.
解答: 连接OA,过点O作OE⊥AB,交⊙O于F,
连接OA,过点O作OE⊥AB,交⊙O于F,
∵圆柱型水管的直径为100cm,
∴AO=FO=50cm,
∵AB=60cm,
∴AE=30cm,
∴OE=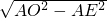 =
= =40(cm),
=40(cm),
∴EF=50-40=10(cm),
故答案为:10cm.
点评:此题主要考查了勾股定理和垂径定理的应用,此类题要构造一个由半径、半弦、弦心距组成的直角三角形,然后根据勾股定理以及垂径定理进行计算.
分析:首先连接OA,过点O作OE⊥AB,交⊙O于F,根据垂径定理,即可求得AE的值,然后在Rt△OAE中,利用勾股定理,即可求得OE的值,继而求得污水的最大深度.
解答:
 连接OA,过点O作OE⊥AB,交⊙O于F,
连接OA,过点O作OE⊥AB,交⊙O于F,∵圆柱型水管的直径为100cm,
∴AO=FO=50cm,
∵AB=60cm,
∴AE=30cm,
∴OE=
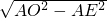 =
= =40(cm),
=40(cm),∴EF=50-40=10(cm),
故答案为:10cm.
点评:此题主要考查了勾股定理和垂径定理的应用,此类题要构造一个由半径、半弦、弦心距组成的直角三角形,然后根据勾股定理以及垂径定理进行计算.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目

 为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为
为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为