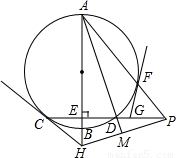
题目内容
(1999•青岛)已知:如图,在菱形ABCD中,BE=DF,DE和CB的延长线相交于G.求证:(1)△ADE≌△CBF;(2)
 .
.
【答案】分析:(1)首先由菱形ABCD的性质得到AD=BC,∠A=∠C,又BE=DF,由此得到AE=CF,然后利用全等三角形的判定方法即可证明△ADE≌△CBF;
(2)由(1)得到DE=BF,根据菱形性质得到AB∥CD,然后利用平行线分线段成比例得到 ,接着即可证明题目结论.
,接着即可证明题目结论.
解答:证明:(1)∵在菱形ABCD中,AD=BC,∠A=∠C,
又∵AB=CD,BE=DF,
∴AE=CF,
∴△ADE≌△CBF;
(2)∵△ADE≌△CBF,
∴DE=BF,
∵在菱形ABCD中,BC=CD,AB∥CD,
∴ ,
,
∴ .
.
点评:此题把菱形、全等三角形、平行线分线段成比例结合起来,综合性比较强,首先利用菱形的性质得到全等三角形,利用全等三角形的性质得到线段相等,再利用平行线分线段成比例解决题目的问题.
(2)由(1)得到DE=BF,根据菱形性质得到AB∥CD,然后利用平行线分线段成比例得到
 ,接着即可证明题目结论.
,接着即可证明题目结论.解答:证明:(1)∵在菱形ABCD中,AD=BC,∠A=∠C,
又∵AB=CD,BE=DF,
∴AE=CF,
∴△ADE≌△CBF;
(2)∵△ADE≌△CBF,
∴DE=BF,
∵在菱形ABCD中,BC=CD,AB∥CD,
∴
 ,
,∴
 .
.点评:此题把菱形、全等三角形、平行线分线段成比例结合起来,综合性比较强,首先利用菱形的性质得到全等三角形,利用全等三角形的性质得到线段相等,再利用平行线分线段成比例解决题目的问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 .
.
 (证明过程中最好用数字表示角).
(证明过程中最好用数字表示角).
 (证明过程中最好用数字表示角).
(证明过程中最好用数字表示角).