题目内容
 已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解为( )
已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解为( )分析:根据图象可以得到:图象与x轴的一个交点是(3,0),对称轴是:x=1,即可求得抛物线与x轴的交点的坐标,交点的横坐标就是方程的解.
解答:解:根据图象可以得到:图象与x轴的一个交点是(3,0),对称轴是:x=1,
(3,0)关于x=1的对称点是:(-1,0).
则抛物线与x轴的交点是:(3,0)和(-1,0).
故于x的一元二次方程ax2+bx+c=0的解为:x1=3,x2=-1.
故选D.
(3,0)关于x=1的对称点是:(-1,0).
则抛物线与x轴的交点是:(3,0)和(-1,0).
故于x的一元二次方程ax2+bx+c=0的解为:x1=3,x2=-1.
故选D.
点评:本题考查了二次函数与x轴的交点与一元二次方程的解的关系,正确求得抛物线与x轴的交点是关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
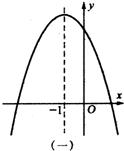 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
