Question

【题目】如图，点E是矩形ABCD的对角线BD上的一点，且BE=BC，AB=3，BC=4，点P为直线EC上的一点，且PQ⊥BC于点Q，PR⊥BD于点R．

（1）①如图1，当点P为线段EC中点时，易证：PR+PQ= （不需证明）．②如图2，当点P为线段EC上的任意一点（不与点E、点C重合）时，其它条件不变，则①中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．

（2）如图3，当点P为线段EC延长线上的任意一点时，其它条件不变，则PR与PQ之间又具有怎样的数量关系？请直接写出你的猜想．

Answer 1

【答案】（1）成立，理由见解析；（2）PR﹣PQ=

【解析】

试题（1）②连接BP，过C点作CK⊥BD于点K．根据矩形的性质及勾股定理求出BD的长，根据三角形面积相等可求出CK的长，最后通过等量代换即可证明；

（2）图3中的结论是PR﹣PQ=．

试题解析：解：（1）②图2中结论PR+PQ=仍成立．

证明：连接BP，过C点作CK⊥BD于点K．

∵四边形ABCD为矩形，∴∠BCD=90°．又∵CD=AB=3，BC=4，∴BD===5．

∵S△BCD=BCCD=BDCK，∴3×4=5CK，∴CK=．

∵S△BCE=BECK，S△BEP=PRBE，S△BCP=PQBC，且S△BCE=S△BEP+S△BCP，∴BECK=PRBE+PQBC．又∵BE=BC，∴CK=PR+PQ，∴CK=PR+PQ．又∵CK=，∴PR+PQ=；

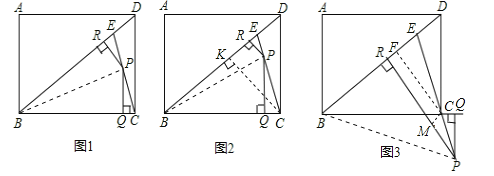
（2）过C作CF⊥BD交BD于F，作CM⊥PR交PR于M，连接BP，S△BPE﹣S△BCP=S△BEC，S△BEC是固定值，BE=BC为两个底，PR，PQ 分别为高，图3中的结论是PR﹣PQ=．