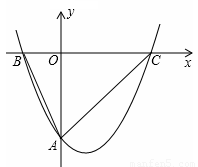
题目内容
如图,经过原点的抛物线 与
与 轴的另一个交点为A.过点
轴的另一个交点为A.过点 作直线
作直线 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥ 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.
(1)当 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当 时,连结CA,问
时,连结CA,问 为何值时
为何值时 ?
?
(3)过点P作 且
且 ,问是否存在
,问是否存在 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.
(1)A(-4,0),BC=2;(2) ;(3)
;(3)
解析试题分析:(1)把m=2代入抛物线的解析式,令y=0解方程,得到的非0解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;
(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到 ,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;
,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;
(3)存在,本题要分当m>1时,BC=2(m-1),PM=m,BP=m-1和当0<m<1时,BC=2(1-m),PM=m,BP=1-m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
(1)当m=2时, ,
,
令y=0,得 ,∴
,∴
∴A(-4,0)
当x=-1时,y=3,∴B(-1,3)
∵抛物线 的对称轴为直线x=-2,
的对称轴为直线x=-2,
又∵B,C关于对称轴对称,
∴BC=2.

∴
∴ ∴
∴ ;
;
(3)∵B,C不重合,∴m≠1.(I)当m>1时,BC=2(m-1),PM=m, BP=m-1.
(i)若点E在x轴上(如图1),
∵∠CPE=90°,∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP. 又∵∠CPB=∠PME=90°,PC=EP
∴△BPC≌△MEP,∴BC=PM, ∴2(m-1)=m,
∴m=2,此时点E的坐标是(-2,0).
(II)当0<m<1时,BC=2(1-m),PM=m, BP=1-m,
(i)若点E在x轴上, 易证△BPC≌△MEP,∴BC=PM,
∴2(1-m)=m,∴ ,此时点E的坐标是
,此时点E的坐标是 ;
;
考点:函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

 阅读快车系列答案
阅读快车系列答案
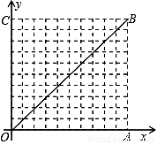
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为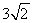
 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )